
| AЃЎ | ЃЈ1ЃЌ$\frac{3}{2}$ЃЉ | BЃЎ | ЃЈ1ЃЌ$\frac{3}{2}$] | CЃЎ | [1ЃЌ$\frac{3}{2}$ЃЉ | DЃЎ | [1ЃЌ$\frac{3}{2}$] |
ЗжЮі ИљОнЗжЪНКЏЪ§КЭЖдЪ§КЏЪ§ЕФЕЅЕїадЕФаджЪЧѓГіКЏЪ§fЃЈxЃЉЕФШЁжЕЗЖЮЇЃЌЧѓКЏЪ§gЃЈxЃЉЕФЕМЪ§gЁфЃЈxЃЉЃЌХаЖЯКЏЪ§gЃЈxЃЉдк[0ЃЌ1]ЩЯЕФЕЅЕїадЃЌИљОнЬѕМўЖдгкШЮвтx1ЁЪ[0ЃЌ1]змДцдкx2ЁЪ[0ЃЌ1]ЃЌЪЙЕУgЃЈx2ЃЉ=fЃЈx1ЃЉГЩСЂЃЌНјаазЊЛЏЧѓНтМДПЩЃЎ
НтД№ НтЃКЕБ0ЁмxЁм$\frac{1}{4}$ЪБЃЌfЃЈxЃЉ=$\frac{3-4x}{2x-1}$=$\frac{-4x+2+1}{2x-1}$=-2+$\frac{1}{2x-1}$ЁЪ[-4ЃЌ-3]ЃЌ
ЕБ$\frac{1}{4}$ЃМxЁм1ЪБЃЌfЃЈxЃЉ=$\frac{1}{2}$log2x-3ЁЪЃЈ-4ЃЌ-3]ЃЌ
злЩЯЕБxЁЪ[0ЃЌ1]ЪБfЃЈxЃЉЁЪ[-4ЃЌ-3]ЃЌ
gЃЈxЃЉЕФЕМЪ§gЁфЃЈxЃЉ=3x2-6ax=3xЃЈx-2aЃЉЃЌ
гЩgЁфЃЈxЃЉ=0ЕУx=0Лђx=2aЃЌ
ЁпaЁн1ЃЌЁр2aЁн2ЃЌ
дђЕБ0ЁмxЁм1ЪБЃЌ]ЃЌgЁфЃЈxЃЉЁм0ЃЛ
ЙЪgЃЈxЃЉ=x3-3a2x-2aдк[0ЃЌ1]ЩЯЪЧМѕКЏЪ§ЃЌ
дђgЃЈ0ЃЉ=-2aЃЌgЃЈ1ЃЉ=1-3a2-2aЃЌ
МД-3a2-2a+1ЁмgЃЈxЃЉЁм-2a
гжЁпfЃЈxЃЉЕФжЕгђЮЊ[-4ЃЌ-3]ЃЛ
ШєЖдгкШЮвтx1ЁЪ[0ЃЌ1]змДцдкx2ЁЪ[0ЃЌ1]ЃЌЪЙЕУgЃЈx2ЃЉ=fЃЈx1ЃЉГЩСЂЃЌ
ЁрgЃЈ1ЃЉЁм-4ЧвgЃЈ0ЃЉЁн-3ЃЛ
МД$\left\{\begin{array}{l}{-3{a}^{2}-2a+1Ём-4}\\{-2aЁн-3}\end{array}\right.$ЃЌМД$\left\{\begin{array}{l}{3{a}^{2}+2a-5Ён0}\\{aЁм\frac{3}{2}}\end{array}\right.$ЃЌ
ЕУ$\left\{\begin{array}{l}{aЁн1ЛђaЁм-\frac{5}{3}}\\{aЁм\frac{3}{2}}\end{array}\right.$ЃЌЕУ1ЁмaЁм$\frac{3}{2}$ЃЌ
МДЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧ[1ЃЌ$\frac{3}{2}$]ЃЌ
ЙЪбЁЃКD
ЕуЦР БОЬтжївЊПМВщКЏЪ§КуГЩСЂЮЪЬтвдМАКЏЪ§жЕгђЕФЧѓЗЈЃЌИљОнЗжЖЮКЏЪ§ЕФБэДяЪНЧѓГіКЏЪ§ЕФжЕгђвдМАРћгУЕМЪ§баОПКЏЪ§ЕФЕЅЕїадКЭзюжЕЪЧНтОіБОЬтЕФЙиМќЃЎПМВщбЇЩњЕФзЊЛЏФмСІЃЎ


 ЦкФЉГхДЬ100ЗжДДаТН№ОэЭъШЋЪдОэЯЕСаД№АИ
ЦкФЉГхДЬ100ЗжДДаТН№ОэЭъШЋЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
| ИпбЊбЙ | ЗЧИпбЊбЙ | змМЦ | |
| ФъСф20ЕН39Ыъ | 12 | c | 100 |
| ФъСф40ЕН60Ыъ | b | 52 | 100 |
| змМЦ | 60 | a | 200 |
| PЃЈk2Ёнk0ЃЉ | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
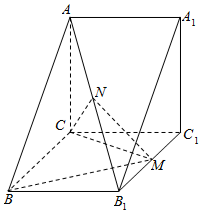 ШчЭМЃЌдкжБШ§РтжљABC-A1B1C1жаЃЌAA1=AC=1ЃЌBC=$\sqrt{2}$ЃЌAB=$\sqrt{3}$ЃЌMЪЧРтB1C1ЕФжаЕуЃЌNЪЧЖдНЧЯпAB1ЕФжаЕуЃЎ
ШчЭМЃЌдкжБШ§РтжљABC-A1B1C1жаЃЌAA1=AC=1ЃЌBC=$\sqrt{2}$ЃЌAB=$\sqrt{3}$ЃЌMЪЧРтB1C1ЕФжаЕуЃЌNЪЧЖдНЧЯпAB1ЕФжаЕуЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌBCЪЧЁбOЕФЧаЯпЃЌBЮЊЧаЕуЃЌOCЦНаагкЯвADЃЌСЌНгCDЃЎ
ШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌBCЪЧЁбOЕФЧаЯпЃЌBЮЊЧаЕуЃЌOCЦНаагкЯвADЃЌСЌНгCDЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $-\frac{7}{8}$ | BЃЎ | $\frac{7}{8}$ | CЃЎ | $\frac{7}{8}$Лђ$-\frac{7}{8}$ | DЃЎ | $\frac{{\sqrt{15}}}{4}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com