
| A. | $\frac{2}{π}$ | B. | $\frac{1}{π}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
分析 利用函数的导数求得f(x)的单调递增区间,f(x)为增函数的概率即为单调增区间的长度比上总长度.
解答 解:f(x)=-8sinx+tanx,
f′(x)=-8cosx+$\frac{1}{co{s}^{2}x}$=$\frac{1-8co{s}^{3}x}{co{s}^{2}x}$,
f(x)为增函数,f′(x)=$\frac{1-8co{s}^{3}x}{co{s}^{2}x}$>0,
∴cosx<$\frac{1}{2}$,又x∈($-\frac{π}{2}$,$\frac{π}{2}$),
∴x∈(-$\frac{π}{2}$,-$\frac{π}{3}$)∪($\frac{π}{3}$,$\frac{π}{2}$),
f(x)为增函数的概率P=$\frac{\frac{π}{6}×2}{π}$=$\frac{1}{3}$.
故答案选:D.
点评 本题考查古典概型,利用导数求出函数的单调区间,并求出其长度,并求出其与总长度的比值,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2+i | B. | 1+2i | C. | 2-i | D. | 1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{2}-1}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源:2017届河北衡水中学高三上学期调研三考数学(文)试卷(解析版) 题型:解答题
已知函数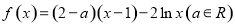 .
.
(1)若曲线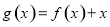 上点
上点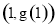 处的切线过点
处的切线过点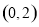 ,求函数
,求函数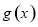 的单调减区间;
的单调减区间;
(2)若函数 在
在 上无零点,求
上无零点,求 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com