Question

【题目】设为实数，已知，

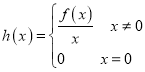
（1）若函数，求的值；

（2）当时，求证：函数在上是单调递增函数；

（3）若对于一切，不等式恒成立，求的取值范围.

Answer 1

【答案】（1）；（2）证明过程见解析；（3）.

【解析】

（1）直接把代入函数解析式，得到方程，求出的值；

（2）求出函数的解析式，用函数单调性的定义进行证明即可；

（3）分类讨论，把函数的解析式，转化为二次函数解析式、分式类型函数解析式形式，利用它们的单调性求出的取值范围.

（1）；

（2），当时，解析式可化简为：

，设是上任意两个不相等的实数，则有，

，

因为，，所以，因此有

，所以函数是上的递增函数；

（3）当时，而，所以，因为，所以有

在恒成立，设，对称轴为：，故在上是增函数，要想（*）恒成立，只需

该不等式恒成立，故；

当时，， 此时函数是单调递增函数，要想在上恒成立，只需这与矛盾，故不成立；

当时，，

当时，函数是单调递增函数，当时，由（2）可知函数是单调递增函数，所以函数在时，最小值为

要想在上恒成立，只需，而，所以，综上所述：的取值范围为：.