
【题目】设函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 仅在
仅在![]() 处有极值,求
处有极值,求![]() 的取值范围;
的取值范围;
(Ⅲ)若对于任意的![]() ,不等式
,不等式![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() ,
,![]() 内是增函数,在
内是增函数,在![]() ,
,![]() 内是减函数.(2)
内是减函数.(2)![]() ;(3)
;(3)![]() .
.
【解析】
(Ⅰ)当![]() 时,
时,![]() ,解不等式
,解不等式![]() 和
和![]() 得到
得到![]() 的增区间和减区间.
的增区间和减区间.
(Ⅱ)![]() ,因
,因![]() 仅在
仅在![]() 取极值,故
取极值,故![]() 恒成立,故可得
恒成立,故可得![]() 的取值范围.
的取值范围.
(Ⅲ)由![]() 可知
可知![]() 恒成立,结合函数的单调性可知
恒成立,结合函数的单调性可知![]() ,故由
,故由![]() 可得
可得![]() 的取值范围.
的取值范围.
(Ⅰ)![]() .
.
当![]() 时,
时,
![]() .
.
令![]() ,解得
,解得![]() ,
,![]() ,
,![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以![]() 在
在![]() ,
,![]() 内是增函数,在
内是增函数,在![]() ,
,![]() 内是减函数.
内是减函数.
(Ⅱ)![]() ,显然
,显然![]() 不是方程
不是方程![]() 的根.
的根.
为使![]() 仅在
仅在![]() 处有极值,必须
处有极值,必须![]() 恒成立,即有
恒成立,即有![]() .
.
解此不等式,得![]() .这时,
.这时,![]() 是唯一极值.
是唯一极值.
因此满足条件的![]() 的取值范围是
的取值范围是![]()
(Ⅲ)由条件![]() 可知
可知![]() ,从而
,从而![]() 恒成立.
恒成立.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此函数![]() 在
在![]() 上的最大值是
上的最大值是![]() 与
与![]() 两者中的较大者.
两者中的较大者.
为使对任意的![]() 不等式
不等式![]() 在
在![]() 上恒成立,当且仅当
上恒成立,当且仅当
![]() 即
即![]()
在![]() 上恒成立,
上恒成立,
所以![]() ,因此满足条件的
,因此满足条件的![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若函数![]() 在
在![]() 处取得极值,求实数
处取得极值,求实数![]() 的值;
的值;
(2)在(1)的结论下,若关于![]() 的不等式
的不等式![]() ,当
,当![]() 时恒成立,求
时恒成立,求![]() 的值;
的值;
(3)令![]() ,若关于
,若关于![]() 的方程
的方程![]() 在
在![]() 内至少有两个解,求出实数
内至少有两个解,求出实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为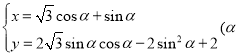 为参数),若以直角坐标系中的原点
为参数),若以直角坐标系中的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车“定速巡航”技术是用于控制汽车的定速行驶,当汽车被设定为定速巡航状态时,电脑根据道路状况和汽车的行驶阻力自动控制供油量,使汽车始终保持在所设定的车速行驶,而无需司机操纵油门,从而减轻疲劳,促进安全,节省燃料.某汽车公司为测量某型号汽车定速巡航状态下的油耗情况,选择一段长度为240km的平坦高速路段进行测试.经多次测试得到一辆汽车每小时耗油量F(单位:L)与速度v(单位:km/h)(![]() )的下列数据:
)的下列数据:
v | 0 | 40 | 60 | 80 | 120 |
F | 0 |
|
| 10 | 20 |
为了描述汽车每小时耗油量与速度的关系,现有以下三种函数模型供选择:
![]() ,
, ,
,![]() .
.
(1)请选出你认为最符合实际的函数模型,并求出相应的函数解析式.
(2)这辆车在该测试路段上以什么速度行驶才能使总耗油量最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修44:坐标系与参数方程]
在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]()
为参数).以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标
的极坐标
方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() .若点
.若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 两点间的距离
两点间的距离![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]()
(1)求![]() 的最小正周期和单调增区间
的最小正周期和单调增区间
(2)求![]() 图象的对称轴的方程和对称中心的坐标
图象的对称轴的方程和对称中心的坐标
(3)在给出的直角坐标系中,请画出![]() 在区间
在区间![]() 上的图象并求其值域.
上的图象并求其值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义域为
是定义域为![]() 的奇函数,且当
的奇函数,且当![]() 时,
时, ![]() ,设
,设![]() “
“![]() ”.
”.
(1)若![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)设![]() 集合
集合![]() 与集合
与集合![]() 的交集为
的交集为![]() ,若
,若![]() 为假,
为假, ![]() 为真,求实数
为真,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com