
| A. | ¬q | B. | (¬p)∨(¬q) | C. | p∧q | D. | p∧(¬q) |
分析 利用函数零点存在定理以及基本不等式分别判断两个命题的真假,然后结合复合命题真假之间的关系是解决本题的关键.
解答 解:设f(x)=ex+x-5,则f(x)=1-5=-4<0,f(5)=e5+5-5=e5>0,
则:?x0∈(0,+∞),使f(x0)=0,即e${\;}^{{x}_{0}}$+x0=5成立,即命题p是真命题,
$\frac{3}{x+1}$+x=$\frac{3}{x+1}$+x+1-1≥2$\sqrt{\frac{3}{x+1}•(x+1)}$-1=2$\sqrt{3}$-1,
当且仅当$\frac{3}{x+1}$=x+1,即x+1=$\sqrt{3}$,x=$\sqrt{3}-1$时取等号,
故:?x∈(0,+∞),$\frac{3}{x+1}$+x≥2$\sqrt{3}$-1成立,即命题q为真命题.
则p∧q为真命题,其余为假命题,
故选:C
点评 本题主要考查复合命题真假之间的关系的判断,利用条件判断p,q的真假性是解决本题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①和② | B. | ①和③ | C. | ②和④ | D. | ①和④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
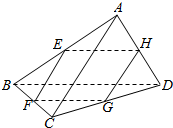 如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.
如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
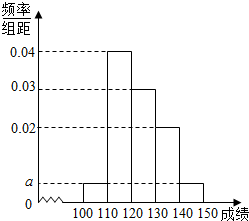 贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示,其中成绩分组区间是[100,110),[110,120),[120,130),[130,140),[140,150].
贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示,其中成绩分组区间是[100,110),[110,120),[120,130),[130,140),[140,150].| 分数段 | [100,110) | [110,120) | [120,130) | [130,140) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
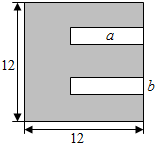 如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )| A. | 1 | B. | $\frac{11}{10}$ | C. | $\frac{6}{5}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com