
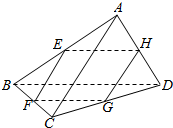
 如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.
如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形. 分析 由已知EH$\underset{∥}{=}$$\frac{1}{2}BD$$\underset{∥}{=}$FG,EF$\underset{∥}{=}$$\frac{1}{2}$AC$\underset{∥}{=}$HG,从而四边形EFGH为平行四边形,由四边形EFGH为菱形,得EF=EH,由此得到AC=BD.
解答 解:在三棱锥A-BCD中,
∵E,F,G,H分别是棱AB,BC,CD,DA的中点,
∴EH$\underset{∥}{=}$$\frac{1}{2}BD$,FG$\underset{∥}{=}$$\frac{1}{2}$BD,∴EH$\underset{∥}{=}$FG,
EF$\underset{∥}{=}$$\frac{1}{2}$AC,HG$\underset{∥}{=}$$\frac{1}{2}$AC,∴EF$\underset{∥}{=}$HG,
∴四边形EFGH为平行四边形,
∵四边形EFGH为菱形,∴EF=EH,∴AC=BD,
∴当AC,BD满足条件AC=BD时,四边形EFGH为菱形.
故答案为:AC=BD.
点评 本题考查四边形为菱形时需要具备条件的求法,是基础题,解题时要认真审题,注意三角形中位线定理和平行公理的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 21 | C. | 24 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬q | B. | (¬p)∨(¬q) | C. | p∧q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,1] | C. | (-∞,1] | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 9 | C. | π2 | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com