
| A. | 20 | B. | 21 | C. | 24 | D. | 25 |
分析 由题意可得,an=$\frac{48}{(n+2)^{2}-4}$=12($\frac{1}{n}$-$\frac{1}{n+4}$),利用裂项求和可得Sn=25-12($\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+$\frac{1}{n+4}$),求出结果再跟选项相比较即可.
解答 解:∵an=$\frac{48}{(n+2)^{2}-4}$=12($\frac{1}{n}$-$\frac{1}{n+4}$)
∴Sn=12(1-$\frac{1}{5}$+$\frac{1}{2}$-$\frac{1}{6}$+$\frac{1}{3}$-$\frac{1}{7}$+$\frac{1}{4}$-$\frac{1}{8}$+…+$\frac{1}{n}$-$\frac{1}{n+4}$)=12(1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$-$\frac{1}{n+3}$-$\frac{1}{n+4}$)=25-12($\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+$\frac{1}{n+4}$)
∴与S98最接近的整数是25;
故选D.
点评 本题主要考查了数列的求和,而求和方法的选择最关键的是观察通项公式,正确裂项.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①和② | B. | ①和③ | C. | ②和④ | D. | ①和④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
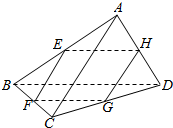 如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.
如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com