
【题目】已知函数![]() 的两个零点为
的两个零点为![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)求证: ![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析: (1)方法一的思路是:求出函数![]() 的最大值,有两个零点,再最大值一定大于零,求出实数
的最大值,有两个零点,再最大值一定大于零,求出实数![]() 的范围.方法二是转化为两个函数的图象有两个交点; (2)采用综合法和分析法证明不等式.构造函数
的范围.方法二是转化为两个函数的图象有两个交点; (2)采用综合法和分析法证明不等式.构造函数![]() ,利用单调性求出
,利用单调性求出![]() 的范围,构造函数
的范围,构造函数![]() ,证明
,证明![]() 在
在![]() 上为增函数,
上为增函数, ![]() ,化简,得证.
,化简,得证.
试题解析:(1)方法一: ![]() ,
,
①![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增,不可能有两个零点.
上单调递增,不可能有两个零点.
②![]() 时,由
时,由![]() 可解得
可解得![]() ,由
,由![]() 可解得
可解得![]() .
.
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,于是
上单调递增,于是![]() .
.
要使得![]() 在
在![]() 上有两个零点,则
上有两个零点,则![]() ,解得
,解得![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.
方法二: ![]() ,可转化为函数
,可转化为函数![]() 与函数
与函数![]() 图象有两个交点.
图象有两个交点.
∵![]() ,∴当
,∴当![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() .即
.即![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴![]() .
.
∴![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.
(2)令![]() ,则
,则![]() ,由题意知方程
,由题意知方程![]() 有两个根
有两个根![]() ,即方程
,即方程![]() 有两个根
有两个根![]() ,不妨设
,不妨设![]() .
.
令![]() ,则
,则![]() ,由
,由![]() 可得
可得![]() ,由
,由![]() 可得
可得![]() ,∴
,∴![]() 时,
时, ![]() 单调递增,
单调递增, ![]() 时,
时, ![]() 单调递减.
单调递减.
根据已知有: ![]() ,要证
,要证![]() ,即证
,即证![]() ,即
,即![]() .
.
即证![]() .令
.令![]() ,下面证
,下面证![]() 对任意的
对任意的![]() 恒成立.
恒成立.
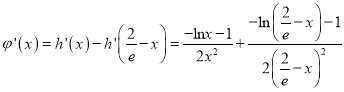 ,∵
,∵![]() ,∴
,∴![]() ,
, ![]() .
.
∴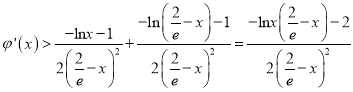 .
.
∵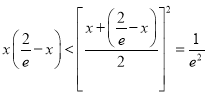 ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() 在
在![]() 是增函数,∴
是增函数,∴![]() ,∴
,∴![]() .
.
点睛: 本题主要考查函数的导数的综合应用,函数的单调性与零点,构造法的应用,考查学生分析问题解决问题的能力,难度比较大.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】已知a>0且a≠1,下列四组函数中表示相等函数的是( )
A.y=logax与y=(logxa)﹣1
B.y=2x与y=logaa2x
C.![]() 与y=x
与y=x
D.y=logax2与y=2logax
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)= 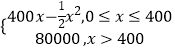 ,其中x是仪器的月产量.(注:总收益=总成本+利润)
,其中x是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润x表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|,g(x)=x+1.
(1)若a=1,求不等式f(x)≤1的解集;
(2)对任意的x∈R,f(x)+|g(x)|≥a2+2a(a>0)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的钢板的边界![]() 是抛物线的一部分,且
是抛物线的一部分,且![]() 垂直于抛物线对称轴,现欲从钢板上截取一块以
垂直于抛物线对称轴,现欲从钢板上截取一块以![]() 为下底边的等腰梯形钢板
为下底边的等腰梯形钢板![]() ,其中
,其中![]() 均在抛物线弧上.设
均在抛物线弧上.设![]() (米),且
(米),且![]() .
.
(1)当![]() 时,求等腰梯形钢板的面积;
时,求等腰梯形钢板的面积;
(2)当![]() 为何值时,等腰梯形钢板的面积最大?并求出最大值.
为何值时,等腰梯形钢板的面积最大?并求出最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果集合A,B,同时满足A∪B={1,2,3,4},A∩B={1},A≠{1},B≠{1},就称有序集对(A,B)为“好集对”.这里有序集对(A,B)意指,当A≠B时,(A,B)和(B,A)是不同的集对,那么“好集对”一共有( )个.
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一企业从某条生产线上随机抽取30件产品,测量这些产品的某项技术指标值![]() ,得到如下的频数分布表:
,得到如下的频数分布表:
|
|
|
|
|
频数 | 2 | 6 | 18 | 4 |
(I)估计该技术指标值的平均数;(用各组区间中点值作代表)
(II) 若![]() 或
或![]() ,则该产品不合格,其余的是合格产品,试估计该条生产线生产的产品为合格品的概率;
,则该产品不合格,其余的是合格产品,试估计该条生产线生产的产品为合格品的概率;
(III)生产一件产品,若是合格品可盈利80元,不合格品则亏损10元,在(II)的前提下,从该生产线生产的产品中任取出两件,记![]() 为两件产品的总利润,求随机变量X的分布列和期望.
为两件产品的总利润,求随机变量X的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com