考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的概念及应用
分析:(1)求导函数,利用导数大于0,求函数的单调增区间,导数小于0,求函数的单调减区间;
(2)对于任意实数x≥1,g(x)≤0恒成立,等价于xlnx+p(x2-1)≤0,设g(x)=xlnx+p(x2-1),由于g(1)=0,故只须g(x)=xlnx+p(x2-1)在x≥1时是减函数,再分离参数p,问题转化为求函数的最小值.
解答:
解:(1)当p=1时,f(x)=ln x-(x-1),f′(x)=
-1,
令f′(x)=0,∴x=1,∵x∈(0,+∞)
故函数f(x)的单调增区间为(0,1),单调减区间为(1,+∞);
(2)由题意函数g(x)=xf(x)+p(2x
2-x-1)=xlnx+p(x
2-1),
则xlnx+p(x
2-1)≤0,
设g(x)=xlnx+p(x
2-1),由于g(1)=0,
故只须g(x)=xlnx+p(x
2-1)在x≥1时是减函数即可,
又因为g′(x)=lnx+2px+1,故lnx+2px+1≤0在x≥1时恒成立,
即p≤-
在x≥1时恒成立,
∵
(-)′=
=0时,x=1.
∴x=1时,-
能取到最小值-
,
∴当p≤-
时,有g(x)≤0.
点评:本题以函数为载体,考查导数的运用,考查利用导数求函数的单调区间,同时考查了函数最值的运用,有一定的综合性.



 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案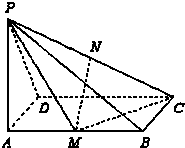 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1