
分析 可先求出$|\overrightarrow{a}|=2,|\overrightarrow{b}|=\frac{2}{\sqrt{3}}$,$\overrightarrow{a}•\overrightarrow{b}=\frac{2\sqrt{3}}{3}$,这样即可根据$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$求出$cos<\overrightarrow{a},\overrightarrow{b}>$的值,从而得出向量$\overrightarrow{a},\overrightarrow{b}$的夹角.
解答 解:$|\overrightarrow{a}|=\sqrt{3+1}=2$,$|\overrightarrow{b}|=\sqrt{1+\frac{1}{3}}=\frac{2}{\sqrt{3}}$,$\overrightarrow{a}•\overrightarrow{b}=\sqrt{3}-\frac{\sqrt{3}}{3}=\frac{2\sqrt{3}}{3}$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{\frac{2\sqrt{3}}{3}}{2×\frac{2}{\sqrt{3}}}=\frac{1}{2}$;
又$0≤<\overrightarrow{a},\overrightarrow{b}>≤π$;
∴$\overrightarrow{a},\overrightarrow{b}$的夹角为$\frac{π}{3}$.
故答案为:2,$\frac{π}{3}$.
点评 考查根据向量坐标求向量长度的方法,向量数量积的坐标运算,以及向量夹角的余弦公式,向量夹角的范围.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:填空题
 如图,在救灾现场,搜救人员从A点出发沿正北方向行进x米到达B处,探测到一个生命迹象,然后从B处沿南偏东75°行进30米到达C处,探测到另一个生命迹象,如果C处恰好在A处的北偏东60°方向上,那么x=10$\sqrt{6}$.米.
如图,在救灾现场,搜救人员从A点出发沿正北方向行进x米到达B处,探测到一个生命迹象,然后从B处沿南偏东75°行进30米到达C处,探测到另一个生命迹象,如果C处恰好在A处的北偏东60°方向上,那么x=10$\sqrt{6}$.米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
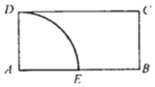 如图,在矩形ABCD中,AD=1,AB=2,以A为圆心,AD为半径在矩形内部作扇形AED,若向矩形ABCD内部随机投放一点,则所投点落在扇形外部的概率为( )
如图,在矩形ABCD中,AD=1,AB=2,以A为圆心,AD为半径在矩形内部作扇形AED,若向矩形ABCD内部随机投放一点,则所投点落在扇形外部的概率为( )| A. | $\frac{π}{8}$ | B. | 1-$\frac{π}{8}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,5) | B. | (1,1) | C. | (3,1) | D. | (3,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x≤2} | B. | {x|0<x≤2且x≠1} | C. | {x|0<x<2} | D. | {x|0<x<2且x≠1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com