
分析 写出二项展开式的通项,由x的指数等于1求得r值,则答案可求.
解答 解:($\sqrt{x}$-$\frac{1}{x}$)5的二项展开式中,通项公式为:
Tr+1=${C}_{5}^{r}$•${(\sqrt{x})}^{5-r}$•${(-\frac{1}{x})}^{r}$=(-1)r•${C}_{5}^{r}$•${x}^{\frac{5-3r}{2}}$,
令$\frac{5-3r}{2}$=1,得r=1;
∴二项式($\sqrt{x}$-$\frac{1}{x}$)5的展开式中含x的一次项系数为:
-1•${C}_{5}^{1}$=-5.
故答案为:-5.
点评 本题考查了二项式系数的性质与应用问题,关键是对二项展开式通项的记忆与应用,是基础题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知函数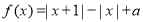 .
.
(1)若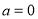 ,求不等式
,求不等式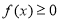 的解集;
的解集;
(2)若方程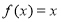 有三个不同的解,求
有三个不同的解,求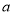 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${x^2}-\frac{y^2}{6}=1$ | B. | ${x^2}-\frac{y^2}{6}=1(x>1)$ | C. | $\frac{x^2}{4}-\frac{y^2}{8}=1(x>2)$ | D. | $\frac{x^2}{4}-\frac{y^2}{8}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{4{e}^{2}}$) | B. | (-$\frac{1}{e}$,$\frac{1}{4{e}^{2}}$)∪(1,+∞) | ||
| C. | (-∞,-$\frac{1}{e}$) | D. | (-∞,-$\frac{1}{e}$)∪(--$\frac{1}{e}$,-$\frac{1}{4{e}^{2}}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com