
分析 (Ⅰ)根据函数奇偶性的定义得到2k+1=0,求出k的值即可;(Ⅱ)根据函数单调性的定义判断即可.
解答 解:(Ⅰ)∵函数F(x)=log2(2x+1)+kx(k为常数)是偶函数,
∴f(-x)=f(x),即 log2( 2-x+1)-kx=log2( 2x+1)+kx,
即log2( 2x+1)-x-kx=log2( 2x+1)+kx,可得(2k+1)x=0,
∴2k+1=0,∴k=-$\frac{1}{2}$;
(Ⅱ)∵f(x)=log2(x+1),g(x)=ex在(-1,+∞)递增,
∴h(x)=f(x)+g(x)在其定义域上单调递增,
不妨设-1<x1<x2,
则h(x1)-h(x2)=log2(x1+1)+${e}^{{x}_{1}}$-log2(x2+1)-${e}^{{x}_{2}}$,
=log2$\frac{{x}_{1}+1}{{x}_{2}+1}$+(${e}^{{x}_{1}}$-${e}^{{x}_{2}}$)
∵x1<x2,
∴$\frac{{x}_{1}+1}{{x}_{2}+1}$<1,${e}^{{x}_{1}}$-${e}^{{x}_{2}}$<0,
故h(x1)-h(x2)<0,
故h(x)在(-1,+∞)递增.
点评 本题考查了函数的单调性和奇偶性问题,考查对数函数以及指数函数的性质,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | -3 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
如图,已知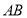 为圆
为圆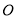 的直径,
的直径,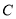 ,
,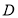 是圆
是圆 上的两个点,
上的两个点,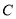 是劣弧
是劣弧 的中点,
的中点,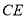 ⊥
⊥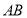 于
于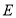 ,
,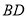 交
交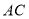 于
于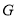 ,交
,交 于
于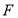 .
.
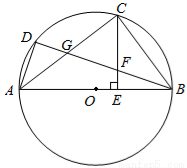
(1)求证: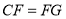 ;
;
(2)求证: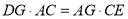 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
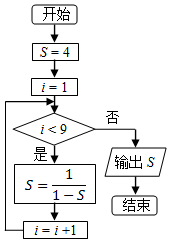
| A. | 4 | B. | $-\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com