
| A. | (-∞,-$\frac{1}{4{e}^{2}}$) | B. | (-$\frac{1}{e}$,$\frac{1}{4{e}^{2}}$)∪(1,+∞) | ||
| C. | (-∞,-$\frac{1}{e}$) | D. | (-∞,-$\frac{1}{e}$)∪(--$\frac{1}{e}$,-$\frac{1}{4{e}^{2}}$) |
分析 函数f(x)在(0,2)上存在两个极值点,等价于f′(x)在(0,2)上有两个零点,
令f′(x)=0,求出x=1和aex+$\frac{1}{{x}^{2}}$=0,且x≠1,x∈(0,2);
求出a=-$\frac{1}{{e}^{x}{•x}^{2}}$,x∈(0,1)∪(1,2);
设t(x)=ex•x2,x∈(0,1)∪(1,2),求出t(x)的取值范围,即得a的取值范围.
解答 解:函数f(x)=a(x-2)ex+lnx+$\frac{1}{x}$在(0,2)上存在两个极值点,
等价于f′(x)=a(x-1)ex+$\frac{1}{x}$-$\frac{1}{{x}^{2}}$在(0,2)上有两个零点,
令f′(x)=0,则a(x-1)ex+$\frac{x-1}{{x}^{2}}$=0,
即(x-1)(aex+$\frac{1}{{x}^{2}}$)=0,
∴x-1=0或aex+$\frac{1}{{x}^{2}}$=0,
∴x=1满足条件,且aex+$\frac{1}{{x}^{2}}$=0(其中x≠1且x∈(0,2));
∴a=-$\frac{1}{{e}^{x}{•x}^{2}}$,其中x∈(0,1)∪(1,2);
设t(x)=ex•x2,其中x∈(0,1)∪(1,2);
则t′(x)=(x2+2x)ex>0,
∴函数t(x)是单调增函数,
∴t(x)∈(0,e)∪(e,4e2),
∴a∈(-∞,-$\frac{1}{e}$)∪(-$\frac{1}{e}$,-$\frac{1}{{4e}^{2}}$).
故选:D.
点评 本题考查了函数导数的综合应用问题,也考查了函数极值与零点的应用问题,考查转化思想与计算能力,是综合性题目.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(文)试卷(解析版) 题型:选择题
已知函数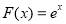 满足
满足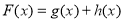 ,且
,且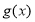 ,
,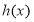 分别是
分别是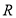 上的偶函数和奇函数,若
上的偶函数和奇函数,若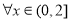 使得不等式
使得不等式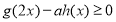 恒成立,则实数
恒成立,则实数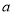 的取值范围是( )
的取值范围是( )
A.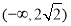 B.
B.
C. D.
D.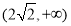
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
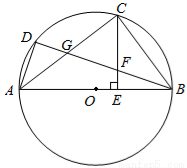
如图,已知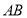 为圆
为圆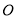 的直径,
的直径,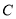 ,
,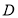 是圆
是圆 上的两个点,
上的两个点,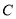 是劣弧
是劣弧 的中点,
的中点,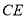 ⊥
⊥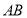 于
于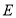 ,
,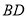 交
交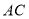 于
于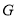 ,交
,交 于
于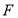 .
.
(1)求证: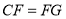 ;
;
(2)求证: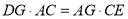 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
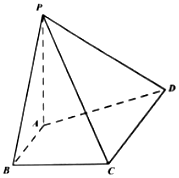 在四菱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.
在四菱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ac>bc | B. | ac>bc | C. | loga(a-c)>logb(b-c) | D. | $\frac{a}{a-c}$>$\frac{b}{b-c}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com