
分析 (1)求导数,利用导数的几何意义,即可求曲线y=f(x)在(1,f(1))处的切线方程;
(2)令$g(x)=({p-1})x-f(x)=({p-1})x-\frac{p}{2}{x^2}+lnx$,求出$g{(x)_{max}}=\frac{1}{2}p-1$.设$h(p)=\frac{{({2p-1})({\frac{1}{2}p-1})}}{{{e^{p-3}}}}({p>1})$,确定单调性,即可证明结论.
解答 解:(1)依题意,f(x)=x2-lnx,故$f'(x)=2x-\frac{1}{x}$,因为f'(1)=1,f(1)=1,故所求切线方程为y=x.
(2)∵p>1,令$g(x)=({p-1})x-f(x)=({p-1})x-\frac{p}{2}{x^2}+lnx$,
故$g'(x)=p-1-px+\frac{1}{x}=\frac{{({px+1})({1-x})}}{x}$,可得函数g(x)的单调递增区间为(0,1),单调递减区间为(1,+∞),
∴g(x)在x=1时取得的极大值,并且也是最大值,即$g{(x)_{max}}=\frac{1}{2}p-1$.
又2p-1>0,∴$({2p-1})[{({p-1})-\frac{p}{2}{x^2}+lnx}]≤({2p-1})({\frac{1}{2}p-1})$.
设$h(p)=\frac{{({2p-1})({\frac{1}{2}p-1})}}{{{e^{p-3}}}}({p>1})$,则$h'(p)=-\frac{{({2{p^2}-9p+7})}}{{2{e^{p-3}}}}=-\frac{{({p-1})({2p-7})}}{{2{e^{p-3}}}}$,
所以h(p)的单调递增区间为$({1,\frac{7}{2}})$,单调递减区间为$({\frac{7}{2},+∞})$,
所以$h(p)≤h({\frac{7}{2}})=\frac{{6×\frac{3}{4}}}{{{e^{\frac{1}{2}}}}}=\frac{9}{{2\sqrt{e}}}$,
∵$2\sqrt{e}>3$,∴$\frac{9}{{2\sqrt{e}}}<\frac{9}{3}=3$,∴h(p)<3,
又∵ep-3>0,∴$({2p-1})[{({p-1})x-\frac{p}{2}{x^2}+lnx}]<3{e^{p-3}}$,即$({p-1})x-f(x)<\frac{{3{e^{p-3}}}}{2p-1}$.
点评 本题考查导数知识的运用,考查不等式的证明,考查学生分析解决问题的能力,正确求导是关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | “x>2”是“x2-2x>0”成立的必要条件 | |
| B. | 命题“若x2=1,则x=1”的逆否命题为假命题 | |
| C. | 命题“p:?x∈R,x2≥0”的否定形式为“¬p:?x0∈R,x02≥0” | |
| D. | .已知向量$\overrightarrow a,\overrightarrow b$,则“$\overrightarrow a∥\overrightarrow b$”是“$\overrightarrow a+\overrightarrow b=\overrightarrow 0$”的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 四棱锥P-ABCD中,底面ABCD是矩形,∠PCD=90°,二面角P-CD-B为60°,BC=1,AB=PC=2.
四棱锥P-ABCD中,底面ABCD是矩形,∠PCD=90°,二面角P-CD-B为60°,BC=1,AB=PC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
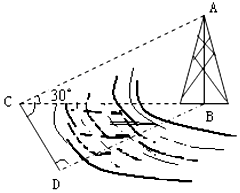 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{3}{2},5}]$ | B. | $[{\frac{2}{3},5}]$ | C. | $[{\frac{3}{2},7}]$ | D. | $[{\frac{2}{3},7}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com