
分析 (Ⅰ)令t=logax,则x=at,可求得f(x)=$\frac{a}{{a}^{2}-1}$(ax-a-x),利用指数函数的单调性质,可判断f(x)=$\frac{a}{{a}^{2}-1}$(ax-a-x)为增函数,且为奇函数,于是当x∈(-1,1)时,f(1-m)+f(1-m2)<0,可得$\left\{\begin{array}{l}{-1≤1-m≤1}\\{{-1≤m}^{2}-1≤1}\\{1-m{<m}^{2}-1}\end{array}\right.$,解之即可求得实数m的范围;
(Ⅱ)由(Ⅰ)知,f(x)=$\frac{a}{{a}^{2}-1}$(ax-a-x)为R上的增函数,故当x∈(-∞,2)时,f(x)<4恒成立?4>f(x)max,即4≥f(2)=$\frac{a}{{a}^{2}-1}$(a2-a-2),于是可求得实数a的取值范围.
解答 解:(Ⅰ)令t=logax,则x=at,f(logax)=$\frac{a}{{a}^{2}-1}$(x-x-1),
可化为:f(t)=$\frac{a}{{a}^{2}-1}$(at-a-t),
即f(x)=$\frac{a}{{a}^{2}-1}$(ax-a-x),
∴当a>1时,$\frac{a}{{a}^{2}-1}$>0,y=g(x)=ax-a-x为增函数,
又g(-x)=-g(x),故y=g(x)=ax-a-x为奇函数,f(x)=$\frac{a}{{a}^{2}-1}$(ax-a-x)为奇函数,
同理,当0<a<1时,f(x)=$\frac{a}{{a}^{2}-1}$(ax-a-x)为增函数.
∵当x∈(-1,1)时,f(1-m)+f(1-m2)<0,
∴f(1-m)<-f(1-m2)=f(m2-1),
∴$\left\{\begin{array}{l}{-1≤1-m≤1}\\{{-1≤m}^{2}-1≤1}\\{1-m{<m}^{2}-1}\end{array}\right.$,解得:1<m≤$\sqrt{2}$.
即实数m的范围为(1,$\sqrt{2}$];
(Ⅱ)由(Ⅰ)知,f(x)=$\frac{a}{{a}^{2}-1}$(ax-a-x)为R上的增函数,
∴当x∈(-∞,2)时,f(x)<4恒成立?4>f(x)max,
又当x∈(-∞,2)时,f(x)取不到最大值,
∴4≥f(2)=$\frac{a}{{a}^{2}-1}$(a2-a-2),即$\frac{a}{{a}^{2}-1}$•$\frac{{(a}^{2}+1){(a}^{2}-1)}{{a}^{2}}$≤4,整理得:a+$\frac{1}{a}$≤4,又a≠1,
解得:2-$\sqrt{3}$≤a<1或1<a≤2+$\sqrt{3}$.
∴实数a的取值范围为[2-$\sqrt{3}$,1)∪(1,2+$\sqrt{3}$].
点评 本题考查函数恒成立问题,考查函数奇偶性与单调性的综合应用,考查等价转化思想与函数方程思想,考查逻辑思维能力与运算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{3}{2},5}]$ | B. | $[{\frac{2}{3},5}]$ | C. | $[{\frac{3}{2},7}]$ | D. | $[{\frac{2}{3},7}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinA)>f(cosB) | B. | f(cosB)>f(sinA) | C. | f(sinA)>f(sinB) | D. | f(cosB)>f(cosA) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
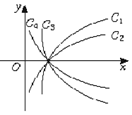 图中曲线是对数函数y=logax的图象,已知a取$\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$四个值,则相应于C1,C2,C3,C4的a值依次为( )
图中曲线是对数函数y=logax的图象,已知a取$\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$四个值,则相应于C1,C2,C3,C4的a值依次为( )| A. | $\frac{4}{3}$,$\sqrt{3}$,$\frac{3}{5}$,$\frac{1}{10}$ | B. | $\sqrt{3}$,$\frac{4}{3}$,$\frac{1}{10}$,$\frac{3}{5}$ | C. | $\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$ | D. | $\frac{4}{3}$,$\sqrt{3}$,$\frac{1}{10}$,$\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com