
【题目】从6名运动员中选4人参加4×100米接力赛,在下列条件下,各有多少种不同的排法?
(1)甲、乙两人必须入选且跑中间两棒;
(2)甲不跑第一棒且乙不跑第四棒.
科目:高中数学 来源: 题型:
【题目】某高三年级学生为了庆祝教师节,同学们为老师制作了一大批同一种规格的手工艺品,这种工艺品有![]()
![]() 两项技术指标需要检测,设各项技术指标达标与否互不影响,若
两项技术指标需要检测,设各项技术指标达标与否互不影响,若![]() 项技术指标达标的概率为
项技术指标达标的概率为![]() 项技术指标达标的概率为
项技术指标达标的概率为![]() ,按质量检验规定:两项技术指标都达标的工艺品为合格品.
,按质量检验规定:两项技术指标都达标的工艺品为合格品.
(1)求一个工艺品经过检测至少一项技术指标达标的概率;
(2)任意依次抽取该工艺品4个,设![]() 表示其中合格品的个数,求
表示其中合格品的个数,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,②复平面上表示
,②复平面上表示![]() 的点在直线
的点在直线![]() 上,③
上,③![]() .这三个条件中任选一个,补充在下面问题中,求出满足条件的复数
.这三个条件中任选一个,补充在下面问题中,求出满足条件的复数![]() ,以及
,以及![]() .已知复数
.已知复数![]() ,
,![]() ,______.若
,______.若![]() ,求复数
,求复数![]() ,以及
,以及![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某课题小组共10人,已知该小组外出参加交流活动次数为1,2,3的人数分别为3,3, 4,现从这10人中随机选出2人作为该组代表参加座谈会.
(1)记“选出2人外出参加交流活动次数之和为4”为事件A,求事件A发生的概率;
(2)设X为选出2人参加交流活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究性学习小组调查研究学生使用智能手机对学习的影响.部分统计数据如下表:
使用智能手机 | 不使用智能手机 | 合计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
合计 | 20 | 10 | 30 |
经计算![]() ,则下列选项正确的是( )
,则下列选项正确的是( )
| 0.50 | 0.25 | 0.1 | 0.050 | 0.010 | 0.005 | 0.001 |
| 0.455 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
A.有99.5%的把握认为使用智能手机对学习有影响
B.有99.5%的把握认为使用智能手机对学习无影响
C.有99.9%的把握认为使用智能手机对学习有影响
D.有99.9%的把握认为使用智能手机对学习无影响
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z满足|z|=![]()
![]() 的虚部为2,z所对应的点在第一象限,
的虚部为2,z所对应的点在第一象限,
(1)求z;
(2)若z,z2,z-z2在复平面上对应的点分别为A,B,C,求cos∠ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.
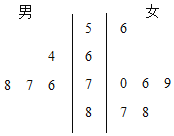
(1)分别计算这10名同学中,男女生测试的平均成绩;
(2)若这10名同学中,男生和女生的国学素养测试成绩的标准差分别为S1,S2,试比较S1与S2的大小(不必计算,只需直接写出结果);
(3)规定成绩大于等于75分为优良,从这10名同学中随机选取一男一女两名同学,求这两名同学的国学素养测试成绩均为优良的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com