
���� ����ƽ�����������㣬��$\overrightarrow{AP}•\overrightarrow{BP}$д�ɣ�$\overrightarrow{OP}-\overrightarrow{OA}$��•��$\overrightarrow{OP}-\overrightarrow{OB}$��=${\overrightarrow{OP}}^{2}+\overrightarrow{OA}•\overrightarrow{OB}-\overrightarrow{OP}•��\overrightarrow{OA}+\overrightarrow{OB}��$=1-$\overrightarrow{OP}•��\overrightarrow{OA}+\overrightarrow{OB}��$�������伸����������ֵ��
���  �⣺����֪�õ�$\overrightarrow{AP}•\overrightarrow{BP}$=��$\overrightarrow{OP}-\overrightarrow{OA}$��•��$\overrightarrow{OP}-\overrightarrow{OB}$��=${\overrightarrow{OP}}^{2}+\overrightarrow{OA}•\overrightarrow{OB}-\overrightarrow{OP}•��\overrightarrow{OA}+\overrightarrow{OB}��$=1-$\overrightarrow{OP}•��\overrightarrow{OA}+\overrightarrow{OB}��$��
�⣺����֪�õ�$\overrightarrow{AP}•\overrightarrow{BP}$=��$\overrightarrow{OP}-\overrightarrow{OA}$��•��$\overrightarrow{OP}-\overrightarrow{OB}$��=${\overrightarrow{OP}}^{2}+\overrightarrow{OA}•\overrightarrow{OB}-\overrightarrow{OP}•��\overrightarrow{OA}+\overrightarrow{OB}��$=1-$\overrightarrow{OP}•��\overrightarrow{OA}+\overrightarrow{OB}��$��
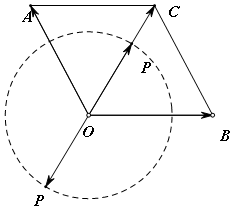
��Ϊ$|{\overrightarrow{OA}}|=2$��$|{\overrightarrow{OB}}|=2$��������$\overrightarrow{OA}$��$\overrightarrow{OB}$�ļн�Ϊ120�㣬����$\overrightarrow{OA}+\overrightarrow{OB}$��ʾ��$\overrightarrow{OA}$��$\overrightarrow{OB}$Ϊ�ڱߵ����εĶԽ��߶�Ӧ������$\overrightarrow{OC}$��
��ͼ
����$\overrightarrow{OP}•\overrightarrow{OC}$�����ֵΪ$|\overrightarrow{OP}||\overrightarrow{OC}|cos0=2\sqrt{3}$����СֵΪ|$|\overrightarrow{OP}||\overrightarrow{OC}|cos��=-2\sqrt{3}$��
����$\overrightarrow{AP}•\overrightarrow{BP}$��ȡֵ��Χ��[1-2$\sqrt{3}$��1+2$\sqrt{3}$]��
�ʴ�Ϊ��[1-2$\sqrt{3}$��1+2$\sqrt{3}$]��
���� ���⿼����ƽ�����������㣬�ؼ��ǽ�������Σ������伸����������ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $2\sqrt{2}-2$ | B�� | $\frac{5}{6}$ | C�� | $3-\frac{3}{2}\sqrt{2}$ | D�� | $2\sqrt{3}-2$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 7 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{13}}{2}$ | B�� | $\frac{3}{2}$ | C�� | 1+$\frac{\sqrt{3}}{2}$ | D�� | $\frac{\sqrt{7}}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com