
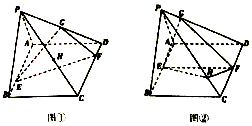
分析 (1)取CD的中点K,连结PK、BK,推导出GF是△DPK的中位线,从而PK∥GF,进而PK∥平面EFG,推导出四边形EBKF是平行四边形,从而BK∥平面EFG,进而平面EFG∥平面PKB,由此能证明PB∥平面EFG.
(2)连结PE,则PE⊥AB,分别以EB、EF、EP所在直线为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角H-EF-G的余弦值.
解答 证明:(1)取CD的中点K,连结PK、BK,
∵G为线段PD的中点,BE=DF=1,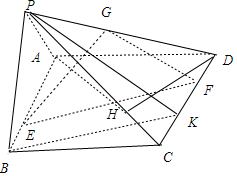
∴GF是△DPK的中位线,∴PK∥GF,
∵GF?平面EFG,PK?平面EFG,
∴PK∥平面EFG,
∵四边形ABCD为正方形,BE=DF=1,∴四边形EBKF是平行四边形,
∴BK∥EF,∵EF?平面EFG,BK?平面EFG,
∴BK∥平面EFG,
∵PK∩BK=K,PK,BK?平面PKB,∴平面EFG∥平面PKB,
∵PB?平面PKB,∴PB∥平面EFG.
解:(2)连结PE,则PE⊥AB,
∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PE?平面PAB,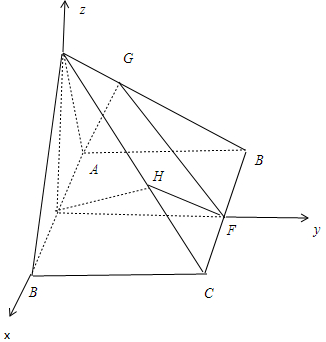
∴PE⊥平面ABCD,分别以EB、EF、EP所在直线为x轴,y轴,z轴,建立空间直角坐标系,
则P(0,0,2$\sqrt{3}$),E(0,0,0),F(0,4,0),G(-$\frac{1}{2}$,1,$\frac{3\sqrt{3}}{2}$),H($\frac{3}{2}$,3,$\frac{\sqrt{3}}{2}$),
则$\overrightarrow{GE}$=($\frac{1}{2},-1,-\frac{3\sqrt{3}}{2}$),$\overrightarrow{EF}$=(0,4,0),$\overrightarrow{HE}$=(-$\frac{3}{2},-3,-\frac{\sqrt{3}}{2}$),
设平面EFG的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{GE}•\overrightarrow{n}=\frac{1}{2}x-y-\frac{3\sqrt{3}}{2}z=0}\\{\overrightarrow{EF}•\overrightarrow{n}=4y=0}\end{array}\right.$,取x=9,得$\overrightarrow{n}$=(9,0,$\sqrt{3}$),
设平面HEF的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{HE}•\overrightarrow{m}=-\frac{3}{2}a-3b-\frac{\sqrt{3}}{2}c=0}\\{\overrightarrow{EF}•\overrightarrow{m}=4b=0}\end{array}\right.$,取a=-1,得$\overrightarrow{m}$=(-1,0,$\sqrt{3}$),
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{-9+3}{\sqrt{81+3}×\sqrt{1+3}}$=-$\frac{\sqrt{21}}{14}$,
由图知二面角H-EF-G是钝角,
∴二面角H-EF-G的余弦值是-$\frac{\sqrt{21}}{14}$.
点评 本题考查线面平行的证明,考查二面角的余弦值的求法,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想、函数与方程思想,考查创新意识、应用意识,是中档题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α内有不共线的三点到β的距离相等; | |
| B. | a内存在直线平行于平面β | |
| C. | 存在平面γ,使得α⊥γ,β⊥γ | |
| D. | 存在异面直线l,m使得l∥α,l∥β,m∥α,m∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,0,1} | B. | {-2,-1,1} | C. | {-1,1,2} | D. | {-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com