
分析 (1)根据抛物线的焦半径公式,求得FD的中点坐标,则$\frac{3\sqrt{2}}{2}$+2+$\frac{(2+\sqrt{2})p}{4}$=3+2$\sqrt{2}$,即可求得p的值,求得抛物线方程;
(2)设直线AB的方程,代入 抛物线方程,由向量平行即韦达定理,即可求得P点坐标,则△EPB为等腰直角三角形,则kAP=1,由直线的斜率公式可得:y1-y2=4,两边平方(y1+y2)2-4y1y2=16,m2=1-x0,x0<1,则d=$\frac{2{x}_{0}}{\sqrt{2-{x}_{0}}}$,根据函数的单调性即可求得点P到直线AB的距离d的取值范围.
解答 解:(1)由题意可知F($\frac{p}{2}$,0),丨FA丨=3+2$\sqrt{2}$+$\frac{p}{2}$,丨FD丨=$\sqrt{2}$丨FA丨=3$\sqrt{2}$+4+$\frac{\sqrt{2}p}{2}$,
则D(3$\sqrt{2}$+4+$\frac{\sqrt{2}p}{2}$+$\frac{p}{2}$,0),FD的中点坐标($\frac{3\sqrt{2}}{2}$+2+$\frac{(2+\sqrt{2})p}{4}$,0),
则$\frac{3\sqrt{2}}{2}$+2+$\frac{(2+\sqrt{2})p}{4}$=3+2$\sqrt{2}$,解得:p=2,
∴抛物线C:y2=4x;
(2)由题意设AB的方程x=my+x0,(m≠0),A(x1,y1),B(x2,y2),E(x2,-y2),
由$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=my+{x}_{0}}\end{array}\right.$,消去x,整理得:y2-4my-4=0,
由x0≥$\frac{1}{2}$,△=16m2+16x0>0,
y1+y2=4m,y1y2=-4x0,
设P(xP,0),则$\overrightarrow{PE}$=(x2-xP,-y2),$\overrightarrow{PA}$=(x1-xP,y1),
由$\overrightarrow{PE}$∥$\overrightarrow{PA}$,则(x2-xP)y1+y2(x1-xP)=0,即x2y1+y2x1=(y1+y2)xP=$\frac{{y}_{2}^{2}{y}_{1}+{y}_{1}^{2}{y}_{2}}{4}$=$\frac{{y}_{1}{y}_{2}({y}_{1}+{y}_{2})}{4}$,显然y1+y2=4m≠0,
∴xP=$\frac{{y}_{1}{y}_{2}}{4}$=-x0,即P(-x0,0),
由题意可知△EPB为等腰直角三角形,
则kAP=1,即$\frac{{y}_{1}+{y}_{2}}{{x}_{1}-{x}_{2}}$=1,则$\frac{{y}_{1}+{y}_{2}}{\frac{1}{4}({y}_{1}^{2}-{y}_{2}^{2})}$=1,则y1-y2=4,
∴(y1+y2)2-4y1y2=16,即16m2+16x0=16,则m2=1-x0,x0<1,
由x0≥$\frac{1}{2}$,则$\frac{1}{2}$≤x0<1,d=$\frac{丨-{x}_{0}-{x}_{0}丨}{\sqrt{1+{m}^{2}}}$=$\frac{2{x}_{0}}{\sqrt{1+{m}^{2}}}$=$\frac{2{x}_{0}}{\sqrt{2-{x}_{0}}}$,
令$\sqrt{2-{x}_{0}}$=t∈(1,$\frac{\sqrt{6}}{2}$],则x0=2-t2,d=$\frac{2(2-{t}^{2})}{t}$=$\frac{4}{t}$-2t,
则f(t)=$\frac{4}{t}$-2t,在(1,$\frac{\sqrt{6}}{2}$]上是减函数,
∴d∈[$\frac{\sqrt{6}}{3}$,2).
点评 本题考查抛物线的性质,直线与抛物线的位置关系,考查向量平行,函数单调性与抛物线的应用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1≥0 | B. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1>0 | ||
| C. | ?x∈R,ex-x-1>0 | D. | ?x∈R,ex-x-1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<2} | B. | {x|0<x≤2} | C. | {x|0≤x<2} | D. | {x|0≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
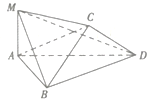 如图,将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD丄平面CBD,若AM丄平面ABD,且AM=$\sqrt{2}$
如图,将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD丄平面CBD,若AM丄平面ABD,且AM=$\sqrt{2}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
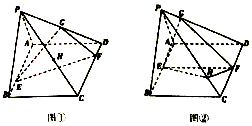
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
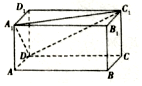 在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,点E在棱AB上移动.
在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,点E在棱AB上移动.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
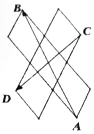
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com