
分析 根据不等式的解法求出命题的等价条件,结合复合命题真假关系进行求解即可.
解答 解:由x2+2x-3>0得x>1或x<-3,即p:x>1或x<-3,
由$\frac{1}{3-x}$>1得$\left\{\begin{array}{l}{3-x>0}\\{1>3-x}\end{array}\right.$,即$\left\{\begin{array}{l}{x<3}\\{x>2}\end{array}\right.$,则2<x<3,
即q:2<x<3,¬q:x≥3或x≤2,
若“(¬q)∧p”为真,
则$\left\{\begin{array}{l}{x>1或x<-3}\\{x≥3或x≤2}\end{array}\right.$,得x≥3或1<x≤2或x<-3,
即x的取值范围是x≥3或1<x≤2或x<-3.
点评 本题主要考查复合命题真假关系的判断,根据不等式的解法求出命题的等价条件是解决本题的关键.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
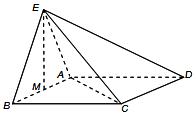 如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点.
如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1≥0 | B. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1>0 | ||
| C. | ?x∈R,ex-x-1>0 | D. | ?x∈R,ex-x-1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{22}{15}$ | B. | $\frac{2}{7}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<2} | B. | {x|0<x≤2} | C. | {x|0≤x<2} | D. | {x|0≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com