
分析 (1)通过绝对值不等式放缩可得结论;
(2)通过当x≠-1时f(x)=$\frac{1}{4}{({x+1})^2}$>0,利用基本不等式的推广放缩可得结论.
解答 (1)证明:因为f(x)=$\frac{1}{4}{({x+1})^2}$≥0,
所以f(x)+|f(x)-2|=|f(x)|+|2-f(x)|≥|f(x)+2-f(x)|=2,
当且仅当f(x)[2-f(x)]≥0即0≤f(x)≤2即-1-2$\sqrt{2}$≤x≤-1+2$\sqrt{2}$时取等号;
(2)解:当x≠-1时,f(x)=$\frac{1}{4}{({x+1})^2}$>0,
所以y=$\frac{1}{4f(x)}+{[{f(x)}]^2}$=$\frac{1}{8f(x)}$+$\frac{1}{8f(x)}$+[f(x)]2≥3•$\root{3}{\frac{1}{8f(x)}•\frac{1}{8f(x)}•[f(x)]^{2}}$=$\frac{3}{4}$,
当且仅当$\frac{1}{8f(x)}$=$\frac{1}{8f(x)}$=[f(x)]2即x=-1±$\sqrt{2}$时取等号,
所以所求最小值为$\frac{3}{4}$.
点评 本题考查函数的最值及其几何意义,考查绝对值不等式,考查基本不等式,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
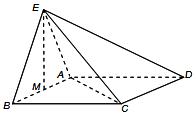 如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点.
如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com