
| A. | $\frac{\sqrt{13}}{2}$ | B. | $\frac{3}{2}$ | C. | 1+$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
分析 由题意对任意x∈R,有|$\overrightarrow{b}+x\overrightarrow{a}$|≥|$\overrightarrow{a}-\overrightarrow{b}$|,两边平方整理.由判别式小于等于0,可得($\overrightarrow{a}-\overrightarrow{b}$)⊥$\overrightarrow{a}$,运用数量积的定义可得即有|$\overrightarrow{a}$|=1,画出$\overrightarrow{AO}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$,建立平面直角坐标系,设出A,B的坐标,求得|t$\overrightarrow{b}$-$\overrightarrow{a}$|+|t$\overrightarrow{b}$-$\frac{\overrightarrow{a}}{2}$|的坐标表示,运用配方和两点的距离公式,结合三点共线,即可得到所求最小值.
解答 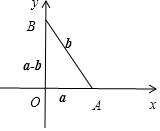 解:向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角为$\frac{π}{3}$,对任意x∈R,有|$\overrightarrow{b}+x\overrightarrow{a}$|≥|$\overrightarrow{a}-\overrightarrow{b}$|,两边平方整理可得x2 ${\overrightarrow{a}}^{2}$+2x$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$-(${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}•\overrightarrow{b}$)≥0,
解:向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角为$\frac{π}{3}$,对任意x∈R,有|$\overrightarrow{b}+x\overrightarrow{a}$|≥|$\overrightarrow{a}-\overrightarrow{b}$|,两边平方整理可得x2 ${\overrightarrow{a}}^{2}$+2x$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$-(${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}•\overrightarrow{b}$)≥0,
则△=4${(\overrightarrow{a}•\overrightarrow{b})}^{2}$+4${\overrightarrow{a}}^{2}$(${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}•\overrightarrow{b}$)≤0,
即有${{(\overrightarrow{a}}^{2}-\overrightarrow{a}•\overrightarrow{b})}^{2}$≤0,即${\overrightarrow{a}}^{2}$=$\overrightarrow{a}•\overrightarrow{b}$,即为($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{a}$.
由向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角为$\frac{π}{3}$,|$\overrightarrow{b}$|=2,可得 ${\overrightarrow{a}}^{2}$=$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos$\frac{π}{3}$=|$\overrightarrow{a}$|•1,∴|$\overrightarrow{a}$|=1.
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{(\overrightarrow{a}-\overrightarrow{b})}^{2}}$=$\sqrt{{\overrightarrow{a}}^{2}{+\overrightarrow{b}}^{2}-2\overrightarrow{a}•\overrightarrow{b}}$=$\sqrt{\sqrt{1+4-2}}$=$\sqrt{3}$.
设$\overrightarrow{OA}$=-$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$,建立平面直角坐标系,如图所示;
则A(1,0),B(0,$\sqrt{3}$),
∴-$\overrightarrow{a}$=(-1,0),$\overrightarrow{b}$=(-1,$\sqrt{3}$);
则|t$\overrightarrow{b}$-$\overrightarrow{a}$|+|t$\overrightarrow{b}$-$\frac{\overrightarrow{a}}{2}$|=$\sqrt{{(1-t)}^{2}{+(\sqrt{3}t)}^{2}}$+$\sqrt{{(\frac{1}{2}-t)}^{2}{+(\sqrt{3}t)}^{2}}$=2( $\sqrt{{(t-\frac{1}{4})}^{2}{+(0-\frac{\sqrt{3}}{4})}^{2}}$+$\sqrt{{(t-\frac{1}{8})}^{2}{+(0+\frac{\sqrt{3}}{8})}^{2}}$),
它表示点P(t,0)与点M($\frac{1}{4}$,$\frac{\sqrt{3}}{4}$)、N($\frac{1}{8}$,$\frac{\sqrt{3}}{8}$)的距离之和,故当P与M、N共线时,
则|t$\overrightarrow{b}$-$\overrightarrow{a}$|+|t$\overrightarrow{b}$-$\frac{\overrightarrow{a}}{2}$|的最小值是2MN=$\frac{\sqrt{7}}{2}$.
点评 本题考查斜率的数量积的定义和性质,主要是向量的平方即为模的平方,考查转化思想和三点共线取得最小值,考查化简整理的运算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 都是增函数 | B. | f(x)为减函数,g(x)为增函数 | ||
| C. | 都是减函数 | D. | f(x)为增函数,g(x)为减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
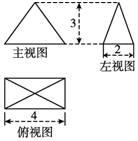
| A. | 8 | B. | 8+4$\sqrt{10}$ | C. | 2$\sqrt{10}$+$\sqrt{13}$ | D. | 4$\sqrt{10}$+2$\sqrt{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com