
分析 (I)先根据平均数求出x的值,再根据中位数的定义即可求出.
(Ⅱ)设轿车分别记为a3,a7,a8,a9,货车记为b7,b8,则从中任拍的两辆的基本事件有15种,拍得轿车、货车各一辆且总成交价格不超过14万元有3种,根据概率公式计算即可.
解答 解:(Ⅰ)由已知$\frac{1}{6}$(3+x+7+9+7+8)=7,解得x=8,
则成交价格的中位数为$\frac{7+8}{2}$=7.5.
(Ⅱ)设轿车分别记为a3,a7,a8,a9,货车记为b7,b8,则从中任拍的两辆的基本事件有a3a7,a3a8,a3a9,a3b7,a3a8,a7a8,a7a9,a7b7,a7a8,a8a9,a8b7,a8a8,
a9b7,a9a8,b7b8,共15种,
拍得轿车、货车各一辆且总成交价格不超过14万元基本事件有a3a7,a3a8,a7b7,共3种,
故拍得轿车、货车各一辆且总成交价格不超过14万元的概率$\frac{3}{15}$=$\frac{1}{5}$.
点评 本题考查了平均数中位数,以及古典概率的问题,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
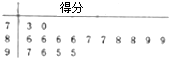 钓鱼岛及其附近海域自古以来就是中国人民进行捕鱼、避风、休息的场所,被誉为深海中的翡翠.某学校就钓鱼岛有关常识随机抽取了16名学生进行测试,用“10分制”以茎叶图方式记录了他们对钓鱼岛的了解程度,分数以小数点前的一位数字为茎,小数点后的一位数字为叶.
钓鱼岛及其附近海域自古以来就是中国人民进行捕鱼、避风、休息的场所,被誉为深海中的翡翠.某学校就钓鱼岛有关常识随机抽取了16名学生进行测试,用“10分制”以茎叶图方式记录了他们对钓鱼岛的了解程度,分数以小数点前的一位数字为茎,小数点后的一位数字为叶.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
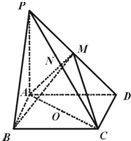 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.若M,N分别为棱PD,PC上的点,O为AC的中点,且AC=2OM=2ON.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.若M,N分别为棱PD,PC上的点,O为AC的中点,且AC=2OM=2ON.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (e,+∞) | B. | [2,e) | C. | $({e+\frac{1}{e},+∞})$ | D. | $[{2,e+\frac{1}{e}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com