
分析 (1)利用已知条件判断轨迹是椭圆,求出a,b即可得到椭圆方程.
(2)利用直线MN斜率不存在时,求解四边形PMQN的面积S=8.当直线MN斜率存在时,设其方程为y=k(x-1)(k≠0),联立方程得$\left\{\begin{array}{l}y=k(x-1)\\{y^2}=4x\end{array}\right.$,设M(x1,y1),N(x2,y2),利用韦达定理,弦长公式,通过PQ⊥MN,推出直线PQ的方程为$y=-\frac{1}{k}(x-1)$,设P(x3,y3),Q(x4,y4),求出|PQ|,推出四边形PMQN的面积利用换元法以及基本不等式求解表达式的最值.
解答 解:(1)设动圆的半径为r,则|CF2|=r,|CF1|=4-r,所以|CF1|+|CF2|=4>|F1F2|,
由椭圆的定义知动圆圆心C的轨迹是以F1,F2为焦点的椭圆,a=2,c=1,所以$b=\sqrt{3}$,动圆圆心C的轨迹方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(2)当直线MN斜率不存在时,直线PQ的斜率为0,易得|MN|=4,|PQ|=4,四边形PMQN的面积S=8.
当直线MN斜率存在时,设其方程为y=k(x-1)(k≠0),联立方程得$\left\{\begin{array}{l}y=k(x-1)\\{y^2}=4x\end{array}\right.$,消元得k2x2-(2k2+4)x+k2=0
设M(x1,y1),N(x2,y2),则$\left\{\begin{array}{l}{x_1}+{x_2}=\frac{4}{k^2}+2\\{x_1}{x_2}=1\end{array}\right.$$|{MN}|=\sqrt{1+{k^2}}\sqrt{{{(\frac{4}{k^2}+2)}^2}-4}=\frac{4}{k^2}+4$
∵PQ⊥MN,∴直线PQ的方程为$y=-\frac{1}{k}(x-1)$,$\left\{\begin{array}{l}y=-\frac{1}{k}(x-1)\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$,得(3k2+4)x2-8x+4-12k2=0
设P(x3,y3),Q(x4,y4),则$\left\{\begin{array}{l}{x_3}+{x_4}=\frac{8}{{3{k^2}+4}}\\{x_1}{x_2}=\frac{{4-12{k^2}}}{{3{k^2}+4}}\end{array}\right.$$|{PQ}|=\sqrt{1+\frac{1}{k^2}}\sqrt{{{(\frac{8}{{3{k^2}+4}})}^2}-4\frac{{4-12{k^2}}}{{3{k^2}+4}}}=\frac{{12({k^2}+1)}}{{3{k^2}+4}}$
四边形PMQN的面积$S=\frac{1}{2}|{MN}||{PQ}|=\frac{1}{2}(\frac{4}{k^2}+4)(\frac{{12({k^2}+1)}}{{3{k^2}+4}})=24\frac{{{{({k^2}+1)}^2}}}{{{k^2}(3{k^2}+4)}}$,
令k2+1=t,t>1,上式$S=24\frac{t^2}{(t-1)(3t+1)}=24[{\frac{1}{3}+\frac{{\frac{2}{3}t+\frac{1}{3}}}{(t-1)(3t+1)}}]$,
令2t+1=z,(z>3),$S=8[{1+\frac{2t+1}{(t-1)(3t+1)}}]=8[{1+\frac{z}{{\frac{z-3}{2}×\frac{3z-1}{2}}}}]=8[{1+\frac{4}{{3(z+\frac{1}{z})-10}}}]$$z+\frac{1}{z}>\frac{10}{3}$(z>3),∴$3(z+\frac{1}{z})-10>0$,∴S>8(1+0)=8,
综上可得S≥8,最小值为8.
点评 本题考查轨迹方程的求法,椭圆的简单性质以及直线与椭圆的位置关系的综合应用,三角形的面积的最值的求法,函数的思想的应用.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P1,P2 | B. | P2,P3 | C. | P3,P4 | D. | P2,P4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
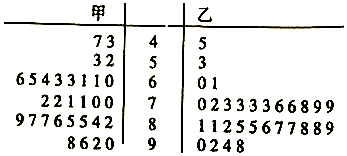
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
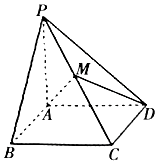 如图所示,已知四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC的中点.
如图所示,已知四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
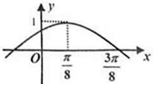 函数f(x)=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的单调递减区间为[$\frac{π}{4}+kπ$,$\frac{5π}{8}+kπ$],k∈Z.
函数f(x)=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的单调递减区间为[$\frac{π}{4}+kπ$,$\frac{5π}{8}+kπ$],k∈Z.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com