
| A�� | P1��P2 | B�� | P2��P3 | C�� | P3��P4 | D�� | P2��P4 |
���� ����Լ���������ǵĿ���������Ŀ�꺯���ļ������壬�����Χ���ж�ѡ������ɣ�
��� �⣺$D=\left\{{\left.{��{x��y}��}\right|\left\{\begin{array}{l}x+y-2��0\\ x-y+2��0\\ 3x-y+6��0\end{array}\right.}\right\}$�Ŀ�������ͼ��
p1��A��-2��0���㣬-2+0=-2��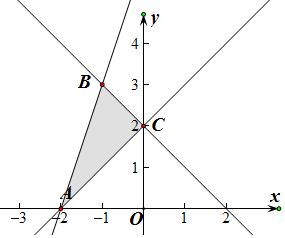 x+y����СֵΪ-2��
x+y����СֵΪ-2��
��?��x��y����D��x+y��0Ϊ�����⣻
p2��B��-1��3���㣬-2-3+1=-4��
A��-2��0����-4-0+1=-3��C��0��2����0-2+1=-1��
��?��x��y����D��2x-y+1��0Ϊ�����⣻
p3��C��0��2���㣬$\frac{2+1}{0-1}$=-3��
��?��x��y����D��$\frac{y+1}{x-1}$��-4Ϊ�����⣻
p4����-1��1���㣬x2+y2=2��
��?��x��y����D��x2+y2��2Ϊ�����⣮
�ɵ�ѡ��p2��p4��ȷ��
��ѡ��D��
���� ���⿼�����Թ滮�Ľ��Ӧ�ã��������ٵ��жϣ���ȷ�����������Լ�Ŀ�꺯���ļ��������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{25}$ | B�� | $\frac{3}{25}$ | C�� | $\frac{1}{5}$ | D�� | $\frac{7}{25}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | $\frac{3}{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
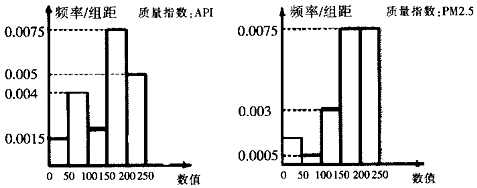
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����p��q�Ǽ����� | B�� | ����p��q�������� | ||
| C�� | ����p�ţ��Vq���Ǽ����� | D�� | ����p�ģ��Vq���������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com