
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,得到f(x)>f(-2),证明结论即可;
(Ⅱ)求出g(x)的导数,得到g(x)的最小值,分离a,得到$\frac{x_0}{{{x_0}+4}}{{e}^{{x_0}+2}}=-a∈(-1,0]$,所以-2<x0≤0.令$u(x)=\frac{1}{x+4}{{e}^{x+2}}(-2<x≤0)$,根据函数的单调性判断即可.
解答 解:(Ⅰ)证明:由$f(x)=\frac{x}{x+4}{e^{x+2}}$,
得$f'(x)=({\frac{4}{{{{(x+4)}^2}}}+\frac{x}{x+4}}){e^{x+2}}=\frac{{{{(x+2)}^2}}}{{{{(x+4)}^2}}}{e^{x+2}}≥0,(x≠-4)$,
故f(x)在(-∞,-4)和(-4,+∞)上单调递增,…(3分)
当x>-2时,由上知f(x)>f(-2)=-1,
即$\frac{x}{x+4}{e^{x+2}}>-1$,即xex+2+x+4>0,得证.…(5分)
(Ⅱ)对$g(x)=\frac{{{{e}^x}-ax-3a}}{{{{(x+2)}^2}}}$求导,
得$g'(x)=\frac{{x{{e}^{x+2}}+a(x+4)}}{{{{(x+2)}^3}}}=\frac{{(x+4)[\frac{x}{x+4}{{e}^{x+2}}+a]}}{{{{(x+2)}^3}}}$,x>-2. …(6分)
记$φ(x)=\frac{x}{x+4}{{e}^{x+2}}+a$,x>-2.
由(Ⅰ)知,函数φ(x)区间(-2,+∞)内单调递增,
又φ(-2)=-1+a<0,φ(0)=a>0,所以存在唯一正实数x0,使得$φ({x_0})=\frac{{{x_0}-2}}{{{x_0}+2}}{{e}^{x_0}}+a=0$.
于是,当x∈(-2,x0)时,φ(x)<0,g'(x)<0,
函数g(x)在区间(-2,x0)内单调递减;
当x∈(x0,+∞)时,φ(x)>0,g'(x)>0,
函数g(x)在区间(x0,+∞)内单调递增.
所以g(x)在(-2,+∞)内有最小值$g({x_0})=\frac{{{{e}^{{x_0}+2}}-a{x_0}-3a}}{{{{({x_0}+2)}^2}}}$,
由题设即$h(a)=\frac{{{{e}^{{x_0}+2}}-a{x_0}-3a}}{{{{({x_0}+2)}^2}}}$. …(9分)
又因为$-a=\frac{x_0}{{{x_0}+4}}{{e}^{{x_0}+2}}$.所以$h(a)=g({x_0})=\frac{1}{{{x_0}+4}}{{e}^{{x_0}+2}}$.
根据(Ⅰ)知,f(x)在(-2,+∞)内单调递增,
$\frac{x_0}{{{x_0}+4}}{{e}^{{x_0}+2}}=-a∈(-1,0]$,所以-2<x0≤0.
令$u(x)=\frac{1}{x+4}{{e}^{x+2}}(-2<x≤0)$,
则$u'(x)=\frac{x+3}{x+4}{{e}^{x+2}}>0$,函数u(x)在区间(-2,0]内单调递增,
所以u(-2)<u(x)≤u(0),
即函数h(a)的值域为$(\frac{1}{2},\frac{{{{e}^2}}}{4}]$. …(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,考查函数恒成立问题,是一道综合题.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:选择题
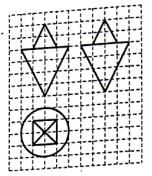
| A. | $\frac{16}{3}(π+1)$ | B. | $\frac{8}{3}(2π+1)$ | C. | 8(2π+1) | D. | 16(π+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P1,P2 | B. | P2,P3 | C. | P3,P4 | D. | P2,P4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
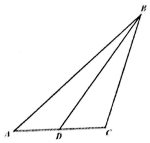 如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且3bsinA=c,D为AC边上一点.
如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且3bsinA=c,D为AC边上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com