练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．以下四个关于圆锥曲线的命题中
    ①设A，B为两个定点，k为非零常数，$|\overrightarrow{PA}|+|\overrightarrow{PB}|=k$，则动点P的轨迹为椭圆；
    ②设定圆C上一定点A作圆的动弦AB，O为坐标原点，若$\overrightarrow{OP}=\frac{1}{2}（\overrightarrow{OA}+\overrightarrow{OB}）$，则动点P的轨迹为圆；
    ③方程ln2x-lnx-2=0的两根可分别作为椭圆和双曲线的离心率；
    ④双曲线$\frac{y^2}{9}-\frac{x^2}{25}=1$与椭圆$\frac{x^2}{35}+{y^2}=1$有相同的焦点．
    其中真命题的序号为②③（写出所有真命题的序号）

    分析 根据题意，依次分析4个命题，对于①、由椭圆的定义分析可得①错误；对于②、分析可得P是AB中点，结合垂径定理分析可得②正确；对于③、求出方程ln2x-lnx-2=0的两根，分析可得两根的大小可得③正确；对于④、分析椭圆、双曲线的焦点位置即可得④不正确，综合即可得答案．

    解答 解：根据题意，依次分析4个命题：
    对于①、若动点P的轨迹为椭圆则需满足k＞|AB|，故①错误；
    对于②、若$\overrightarrow{OP}=\frac{1}{2}（\overrightarrow{OA}+\overrightarrow{OB}）$，则P是AB中点，即∠CPA=90°，所以P的轨迹是以CA为直径的圆，故②正确；
    对于③、方程ln2x-lnx-2=0的两根分别为x=e2或$\frac{1}{e}$，而$\frac{1}{e}＜1，{e^2}＞1$，故③正确；
    对于④、双曲线焦点在y轴上，椭圆的焦点在x轴上；故④不正确
    故答案为：②③．

    点评 本题考查常见圆锥曲线的定义以及简单性质，关键是熟练掌握椭圆、双曲线、抛物线的地定义．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    16．已知抛物线C：y2=4x的焦点为F，过点F且倾斜角为$\frac{π}{3}$的直线与抛物线C的准线交于点B，则线段FB的长为（　　）
    A．10B．6C．8D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．在△ABC中，a，b，c分别为角A，B，C的对边，已知a=2且bcosC+ccosB=2b，则b=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知函数f（x）=x3+sinx+m-3是定义在[n，n+6]上的奇函数，则m+n=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．若直线y=x上存在点（x，y）满足约束条件$\left\{\begin{array}{l}x+y-4≤0\\ x-2y-3≤0\\ x≥m\end{array}\right.$，则实数m的最大值为（　　）
    A．-1B．1C．$\frac{3}{2}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知函数$f（x）=\left\{\begin{array}{l}m{log_{2017}}x+3sinx，x＞0\\{log_{2017}}（-x）+nsinx，x＜0\end{array}\right.$为偶函数，则m-n=（　　）
    A．4B．2C．-2D．-4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=$\frac{x}{x+4}{e^{x+2}}$．
    （I）讨论函数的单调性，并证明当x＞-2时，xex+2+x+4＞0；
    （Ⅱ）证明：当a∈[0，1）时，函数g（x）=$\frac{{{e^{x+2}}-ax-3a}}{{{{（x+2）}^2}}}$（x＞-2）有最小值，设g（x）最小值为h（a），求函数h（a）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一条渐近线的方程为y=x，则该双曲线的离心率e=$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

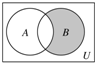    16．已知全集U=Z，A={x∈Z|x2-x-2＜0}，B={-1，0，1，2}，则图中阴影部分所表示的集合等于（　　）
    A．{-1，2}B．{-1，0}C．{0，1}D．{1，2}

    查看答案和解析>>

    同步练习册答案