
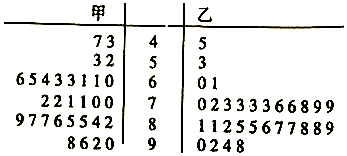
分析 (Ⅰ)由从这两所学校的参赛学生中分别随机抽取30名学生的成绩(百分制)作为样本,乙校每位学生被抽取的概率为0.15,能求出乙校参赛学生总人数.
(Ⅱ)由茎叶图知甲的数据位于茎叶图的左上方偏多,乙的数据位于茎叶图的右下方多,甲的数据相对于乙较分散,乙的数据相对于甲较集中,能从从平均水平与波动情况两个方面分析甲、乙两校参赛学生成绩.
(Ⅲ)记甲校成绩低于60分的4人为1,2,3,4,乙校成绩低于60分的2人为5,6,由此利用列举法能求出3人不在同一学校的概率.
解答 解:(Ⅰ)∵从这两所学校的参赛学生中分别随机抽取30名学生的成绩(百分制)作为样本,
乙校每位学生被抽取的概率为0.15,
∴乙校参赛学生总人数为:30÷0.15=200(人);
(Ⅱ)由茎叶图知甲的数据位于茎叶图的左上方偏多,
乙的数据位于茎叶图的右下方多,
甲的数据相对于乙较分散,乙的数据相对于甲较集中,
∴平均水平:甲小乙大;波动情况:甲大乙小.
(Ⅲ)记甲校成绩低于60分的4人为1,2,3,4,
乙校成绩低于60分的2人为5,6,
则从中选出3人的所有基本事件为:123,124,125,126,134,135,136,145,146,
156,234,235,236,245,246,256,345,346,356,456,共计20个.
记“抽取的3人不在同一学校”为事件A,则A包含的基本事件(用下划线标记)有:
125,126,135,136,145,146,156,235,236,245,246,256,345,346,356,456,共计16个.
∴3人不在同一学校的概率$P(A)=\frac{16}{20}=\frac{4}{5}$.
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | ±2 | D. | ±4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com