
| 父亲身高x(cm) | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y(cm) | 175 | 175 | 176 | 177 | 177 |
分析 根据所给的数据计算出x,y的平均数和回归直线的斜率,即可写出回归直线方程.
解答 解:∵$\overline{x}$176,$\overline{y}$=176,
∴样本组数据的样本中心点是(176,176),
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{1}{2}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=88,
∴回归直线方程为$y=\frac{1}{2}x+88$.
故答案为$y=\frac{1}{2}x+88$
点评 本题考查回归分析的初步应用,写方程要用的斜率和x,y的平均数都要经过计算算出,这样的题有一定的运算量,是一个基础题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,已知△ABC中,D为边BC上靠近B点的三等分点,连接AD,E为线段AD的中点,若$\overrightarrow{CE}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则m+n=$-\frac{1}{2}$.
如图,已知△ABC中,D为边BC上靠近B点的三等分点,连接AD,E为线段AD的中点,若$\overrightarrow{CE}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则m+n=$-\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
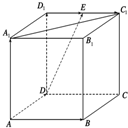
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}f(-\frac{π}{3})<f(\frac{π}{4})$ | B. | $\sqrt{2}f(-\frac{π}{3})<f(-\frac{π}{4})$ | C. | $f(0)>\sqrt{2}f(-\frac{π}{4})$ | D. | $f(\frac{π}{6})<\sqrt{3}f(\frac{π}{3})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com