
 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:填空题
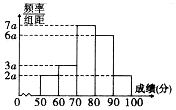 在某市举办的安全教育知识竞赛中,抽取1800名学生的成绩(单位:分),其频率分布直方图如图所示,则成绩落在[50,60)中的学生人数为180.
在某市举办的安全教育知识竞赛中,抽取1800名学生的成绩(单位:分),其频率分布直方图如图所示,则成绩落在[50,60)中的学生人数为180.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{5π}{6}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{5π}{6}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\{\sqrt{3}\}$ | B. | $\{\frac{{\sqrt{3}}}{3}\}$ | C. | $\{\frac{{\sqrt{3}}}{3},\sqrt{3}\}$ | D. | $\{\sqrt{3},3\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图古铜钱外圆内方,外圆直径为4cm,中间是边长为1cm的正方形孔,随机地在古铜钱所在圆内任取一点,则该点刚好位于孔中的概率是$\frac{1}{4π}$.
如图古铜钱外圆内方,外圆直径为4cm,中间是边长为1cm的正方形孔,随机地在古铜钱所在圆内任取一点,则该点刚好位于孔中的概率是$\frac{1}{4π}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com