考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)把b=4代入函数解析式,求出函数的导函数,由导函数的零点对定义域分段,由导函数在各区间段内的符号判断原函数的单调性,从而求得极值;
(2)求出原函数的导函数,由导函数在区间(0,
)上大于等于0恒成立,得到
b≤对任意x∈(0,
)恒成立.由单调性求出
的范围得答案.
解答:
解:(1)当b=4时,f(x)=(x
2+4x+4)
=
(x+2)2(x
≤),
则
f′(x)=2(x+2)+(x+2)2•(1-2x)-•(-2)=
.
由f′(x)=0,得x=-2或x=0.
当x<-2时,f′(x)<0,f(x)在(-∞,-2)上为减函数.
当-2<x<0时,f′(x)>0,f(x)在(-2,0)上为增函数.
当0<x<
时,f′(x)<0,f(x)在(0,
)上为减函数.
∴当x=-2时,f(x)取极小值为0.
当x=0时,f(x)取极大值为4;
(2)由f(x)=(x
2+bx+b)
,得:
f′(x)=(2x+b)+(x2+bx+b)•(1-2x)-•(-2)=
.
由f(x)在区间(0,
)上单调递增,
得f′(x)≥0对任意x∈(0,
)恒成立.
即-5x
2-3bx+2x≥0对任意x∈(0,
)恒成立.
∴
b≤对任意x∈(0,
)恒成立.
∵
>=.
∴
b≤.
∴b的取值范围是
(-∞,].
点评:本题考查了利用导数研究函数的单调性,考查了利用导数求函数的极值,考查了数学转化思想方法,是中档题.



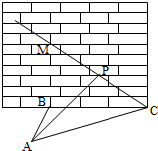 如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小(仰角θ为直线AP与平面ABC所成的角).若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是( )
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小(仰角θ为直线AP与平面ABC所成的角).若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是( )