练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
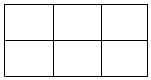
    5．从6个正方形拼成的12个顶点（如图）中任取3个顶点作为一组，其中可以构成三角形的组数为（　　）
    A．208B．204C．200D．196

    分析 根据题意，用间接法，首先计算从12个顶点中任取3个的取法数目，再分析其中不能组成三角形即取出的三点共线的情况，有3种：①三点都在三条水平边上，②三点都在三条竖直边上，③三点在正方形的对角线方向上，分别求出其情况数目，可得能组成三角形的点的组数，进而可得可以构成三角形的组数．

    解答 解：根据题意，从12个顶点中任取3个，有C123=220种取法，
    而其中不能组成三角形即取出的三点共线的情况有：
    ①三点都在三条水平边上，有3C43=12种，
    ②三点都在三条竖直边上，有3C33=4种，
    ③三点在正方形的对角线方向上，如图，有4种情况，
    则不能组成三角形即取出的三点共线的情况有12+4+4=20种；
    则可以构成三角形的组数为220-20=200组；
    故选：C．

    点评 本题考查排列、组合的运用，解题时可用间接法，避免分类讨论，注意三点共线的情况不能有遗漏．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．在△ABC中，角A，B，C所对的边分别为a，b，c，若c2=（a+b）2-6，C=60°，则△ABC的面积是（　　）
    A．$\frac{\sqrt{3}}{2}$B．$\sqrt{3}$C．$\frac{3\sqrt{3}}{2}$D．3$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．写出下面数列{an}的前5项：
    （1）a1=-1，an+1=an+2；
    （2）a1=2，an=$\frac{1}{2}$an+1（n≥1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．函 数y=$\frac{{x}^{2}-x+n}{{x}^{2}+1}$（n∈N*，y≠1）的最大值为an，最小值为bn且cn=4（anbn-$\frac{1}{2}$）
    （1）求数列{cn}的通项公式；
    （2）求f（n）=$\frac{{c}_{n}}{（n+36）{c}_{n+1}}$（n∈N*）的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知A={0，1，2}，B={-1，3}，记：A+B={a+b|a∈A，b∈B}，试用列举法表示A+B={-1，0，1，3，4，5}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知m∈R，要使函数f（x）=|x2-4x+9-2m|+2m在区间[0，4]上的最大值是9，则m的取值范围是（-∞，$\frac{7}{2}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知 f（x）=$\frac{1}{4}$x2+sin（$\frac{5π}{2}$+x），f′（x）为f（x）的导函数，则 y=f′（x）的图象大致是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知二次函数f（x）满足f（2+x）=f（2-x），且f（x）在[0，2]上是增函数，若f（a）≥f（0），则实数a的取值范围是（　　）
    A．[0，+∞）B．（-∞，0]C．（-∞，0]∪[4，+∞）D．[0，4]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．某校三位学生参加省举行的数学团体竞赛，对于其中一题，他们各自解出的概率分别是$\frac{1}{5}，\frac{1}{3}，\frac{1}{4}$，则此题能解出的概率是（　　）
    A．$\frac{1}{60}$B．$\frac{3}{20}$C．$\frac{13}{30}$D．$\frac{3}{5}$

    查看答案和解析>>

    同步练习册答案