已知函数f(x)=ax2+bx+c(a>b>c),满足f(1)=0,且a2+[f(m1)+f(m2)]•a+f(m1)•f(m2)=0.
(1)求证a>0,c<0且b≥0;
(2)求证f(x)的图象被x轴所截得的线段长的取值范围是[2,3);问能否得出f(m1+3),f(m2+3)中至少有一个为正数,请证明你的结论.
证明:(1)∵函数f(x)=ax
2+bx+c(a>b>c),满足f(1)=0,
∴a+b+c=0.(1分)
若a≤0,∵a>b>c∴b<0,c<0,
则有a+b+c<0,这与a+b+c=0矛盾,∴a>0成立.(2分)
若c≥0,则有b>0,a>0,此时a+b+c>0,这与a+b+c=0矛盾,
∴c<0成立.(3分)
∵a
2+[f(m
1)+f(m
2)]•a+f(m
1)•f(m
2)=0
∴[a+f(m
1)]•[a+f(m
2)]=0,∴m
1,m
2是方程f(x)=-a的两根
∴△=b
2-4a(a+c)=b(b+4a)=b(3a-c)≥0
而a>0,c<0∴3a-c>0,
∴b≥0.(4分)
(2)f(1)=0,∴1是方程f(x)=0的一个根,
设x
1=1,另一个根为x
2,有
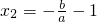
,
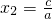
.
∵b=-a-c≥0,a>0,∴
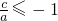
;
又a>0,a>-a-c>c,∴-2<

≤-1,
∴
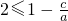
<3,即2≤|x
1-x|<3,
故f(x)的图象被x轴所截得的线段长的取值范围是[2,3).(8分)
设
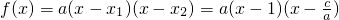
由已知f(m
1)=-a或f(m
2)=-a,不妨设f(m
1)=-a
则
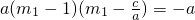
<0,∴

<m
1<1
∴m
1+3>

+3>1,
∴f(m
1+3)>f(1)>0,
同理当f(m
2)=-a,有f(m
2+3)>0,
所以f(m
1+3),f(m
2+3)中至少有一个为正数.(12分)
分析:(1)由习惯性左中函数f(x)=ax
2+bx+c(a>b>c),满足f(1)=0,即a+b+c=0,我们可用反证法来证明a>0,c<0且b≥0;
(2)由f(1)=0,我们可得(1,0)是f(x)的图象与x轴的一个交点,我们由韦达定理及(1)中结论,确定出另一个根的范围,进而得到答案;
点评:本题考查的知识点是二次函数的性质,熟练掌握二次函数的性质,及二次方程与二次函数的关系是解答本题的关键.

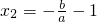 ,
,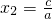 .
.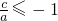 ;
; ≤-1,
≤-1,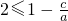 <3,即2≤|x1-x|<3,
<3,即2≤|x1-x|<3,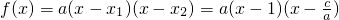
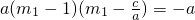 <0,∴
<0,∴ <m1<1
<m1<1 +3>1,
+3>1,
