
【题目】将函数 ![]() 的图象向左平移
的图象向左平移 ![]() 个单位,再向下平移4个单位,得到函数g(x)的图象,则函数f(x)的图象与函数g(x)的图象( )
个单位,再向下平移4个单位,得到函数g(x)的图象,则函数f(x)的图象与函数g(x)的图象( )
A.关于点(﹣2,0)对称
B.关于点(0,﹣2)对称
C.关于直线x=﹣2对称
D.关于直线x=0对称
【答案】B
【解析】解:函数 ![]() 令
令 ![]() (k∈Z),
(k∈Z),
解得x= ![]()
∴对称中心坐标是( ![]() ,0)
,0)
函数 ![]() 的图象向左平移
的图象向左平移 ![]() 个单位,再向下平移4个单位,可得g(x)=3sin(3x+
个单位,再向下平移4个单位,可得g(x)=3sin(3x+ ![]() )﹣4
)﹣4
令3x+ ![]() =kπ(k∈Z),
=kπ(k∈Z),
解得x= ![]()
∴对称中心坐标是( ![]() ,﹣4)
,﹣4)
对称中心不相同,故C,D选项不对.
两个函数对称的纵坐标为﹣2,故A不对.
故选B.
【考点精析】通过灵活运用函数y=Asin(ωx+φ)的图象变换,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象即可以解答此题.
的图象即可以解答此题.


科目:高中数学 来源: 题型:
【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差 x (℃) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是:先用2、3、4、5月的4组数据求线性回归方程,再用1月和6月的2组数据进行检验.
(1)请根据2、3、4、5月的数据,求出y关于x的线性回归方程![]()
![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考公式:  ,
, ![]()
 )
)
参考数据:11×25+13×29+12×26+8×16=![]() 1092,112+132+122+82=498.
1092,112+132+122+82=498.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象与函数y=x3﹣3x2+2的图象关于点( ![]() ,0)对称,过点(1,t)仅能作曲线y=f(x)的一条切线,则实数t的取值范围是( )
,0)对称,过点(1,t)仅能作曲线y=f(x)的一条切线,则实数t的取值范围是( )
A.(﹣3,﹣2)
B.[﹣3,﹣2]
C.(﹣∞,﹣3)∪(﹣2,+∞)
D.(﹣∞,﹣3)∪[﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系的极点在平面直角坐标系的原点O处,极轴与x轴的正半轴重合,两坐标系单位长度相同.已知曲线的极坐标方程为ρ=2cosθ+2sinθ,直线l的参数方程为 ![]() (t为参数).
(t为参数).
(Ⅰ)将直线l的参数方程化为普通方程,将曲线C的极坐标方程化为直角坐标方程;
(Ⅱ)设曲线C上到直线l的距离为d的点的个数为f(d),求f(d)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)在R上的导函数为f'(x),对于任意的实数x,都有f'(x)+2017<4034x,若f(t+1)<f(﹣t)+4034t+2017,则实数t的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型企业甲产品生产的投入成本![]() (单位:万元)与产品销售收入
(单位:万元)与产品销售收入![]() (单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
(单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本20万元的毛利率更大还是投入成本24万元的毛利率更大(![]() )?
)?
相关公式: 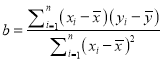
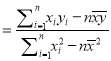 ,
, ![]() .
.
【答案】(1)![]() .(2)投入成本20万元的毛利率更大.
.(2)投入成本20万元的毛利率更大.
【解析】试题分析:(1)由回归公式,解得线性回归方程为![]() ;(2)当
;(2)当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,当
,当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,故投入成本20万元的毛利率更大。
,故投入成本20万元的毛利率更大。
试题解析:
(1)![]() ,
, ![]() ,
,
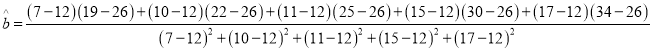
![]() ,
, ![]() ,故
,故![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
(2)当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,
,
当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,
,
故投入成本20万元的毛利率更大.
【题型】解答题
【结束】
21
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() .设椭圆
.设椭圆![]() 的焦点恰为椭圆
的焦点恰为椭圆![]() 短轴的顶点,且椭圆
短轴的顶点,且椭圆![]() 过点
过点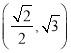 .
.
(1)求![]() 的方程及离心率;
的方程及离心率;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个关于圆锥曲线的命题中:
①设A、B为两个定点,K为非零常数,若|PA|-|PB|=K,则动点P的轨迹是双曲线.
②方程![]() 的两根可分别作为椭圆和双曲线的离心率.
的两根可分别作为椭圆和双曲线的离心率.
③双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点.
有相同的焦点.
④已知抛物线![]() ,以过焦点的一条弦AB为直径作圆,则此圆与准线相切.
,以过焦点的一条弦AB为直径作圆,则此圆与准线相切.
其中真命题为_________(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)若一组斜率为![]() 的平行线,当它们与椭圆
的平行线,当它们与椭圆![]() 相交时,证明:这组平行线被椭圆
相交时,证明:这组平行线被椭圆![]() 截得的线段的中点在同一条直线上.
截得的线段的中点在同一条直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com