Question

【题目】极坐标系的极点在平面直角坐标系的原点O处，极轴与x轴的正半轴重合，两坐标系单位长度相同．已知曲线的极坐标方程为ρ=2cosθ+2sinθ，直线l的参数方程为 （t为参数）．
（Ⅰ）将直线l的参数方程化为普通方程，将曲线C的极坐标方程化为直角坐标方程；
（Ⅱ）设曲线C上到直线l的距离为d的点的个数为f（d），求f（d）的解析式．

Answer 1

【答案】解：（Ⅰ）直线l的参数方程为 （t为参数），消去参数，可得普通方程x+y﹣1=0；
曲线的极坐标方程为ρ=2cosθ+2sinθ，即ρ2=2ρcosθ+2ρsinθ，∴x2+y2﹣2x﹣2y=0；
（Ⅱ）x2+y2﹣2x﹣2y=0，可化为（x﹣1）2+（y﹣1）2=2，
圆心C（1，1）到直线l的距离为 = ，圆的半径为 ，
圆上的点到直线l距离d的取值范围是0≤d≤
∴f（d）=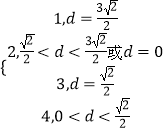
【解析】（Ⅰ）将直线l的参数方程消去参数，可得普通方程，将曲线C的极坐标方程，即ρ2=2ρcosθ+2ρsinθ，即可化为直角坐标方程；（Ⅱ）圆心C（1，1）到直线l的距离为 = ，圆的半径为 ，圆上的点到直线l距离d的取值范围是0≤d≤ ，即可求f（d）的解析式．