
分析 (1)由f(x)=$\frac{{x}^{2}}{1+{x}^{2}}$=1-$\frac{1}{{x}^{2}+1}$,能求出求f(2)与f($\frac{1}{2}$),f(3)与f($\frac{1}{3}$)的值.
(2)由f(x)=$\frac{{x}^{2}}{1+{x}^{2}}$,能证明f(x)+f($\frac{1}{x}$)=1.
解答 解:(1)由f(x)=$\frac{{x}^{2}}{1+{x}^{2}}$=1-$\frac{1}{{x}^{2}+1}$,
∴f(2)=1-$\frac{1}{{2}^{2}+1}$=$\frac{4}{5}$,f($\frac{1}{2}$)=1-$\frac{1}{\frac{1}{4}+1}$=$\frac{1}{5}$.
f(3)=1-$\frac{1}{{3}^{2}+1}$=$\frac{9}{10}$,f($\frac{1}{3}$)=1-$\frac{1}{\frac{1}{9}+1}$=$\frac{1}{10}$.
证明:(2)∵f(x)=$\frac{{x}^{2}}{1+{x}^{2}}$,
∴f(x)+f($\frac{1}{x}$)=$\frac{{x}^{2}}{1+{x}^{2}}$+$\frac{\frac{1}{{x}^{2}}}{1+\frac{1}{{x}^{2}}}$
=$\frac{{x}^{2}}{1+{x}^{2}}$+$\frac{1}{{x}^{2}+1}$=1.
故f(x)+f($\frac{1}{x}$)=1.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
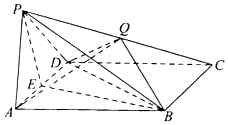 已知四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.
已知四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com