
分析 (1)运用配方法,令t=x-2,可得f(t)的解析式,即有f(x)的解析式;
(2)求得g(x)=f(x)-bx=x2-bx+5,由于f(x)的图象开口向上,可得f(x)的最大值在区间的端点处取得,分别考虑,解方程可得b的值,注意检验对称轴和区间的关系.
解答 解:(1)f(x-2)=x2-4x+9=(x-2)2+5,
令t=x-2,则f(t)=t2+5,
即有f(x)=x2+5;
(2)g(x)=f(x)-bx=x2-bx+5,
当$x∈[{\frac{1}{2}\;,\;\;1}]$时,g(x)的最大值为$\frac{11}{2}$,
由于f(x)的图象开口向上,可得f(x)的最大值在区间的端点处取得,
若f(1)取得最大值,即为1-b+5=$\frac{11}{2}$,
解得b=$\frac{1}{2}$,
则f(x)=x2-$\frac{1}{2}$x+5,对称轴为x=$\frac{1}{4}$,1与对称轴的距离大于$\frac{1}{2}$与对称轴的距离,
则f(1)取得最大值成立;
若f($\frac{1}{2}$)取得最大值,即为$\frac{1}{4}$-$\frac{1}{2}$b+5=$\frac{11}{2}$,
解得b=-$\frac{1}{2}$,
则f(x)=x2+$\frac{1}{2}$x+5,对称轴为x=-$\frac{1}{4}$,1与对称轴的距离大于$\frac{1}{2}$与对称轴的距离,
则f(1)取得最大值成立,故该情况不成立.
综上可得,b=$\frac{1}{2}$.
点评 本题考查二次函数的解析式的求法,注意运用换元法,考查二次函数在闭区间上的最值的求法,注意考虑对称轴与区间的关系,考查化简整理的运算能力,属于中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10元 | B. | 15元 | C. | 20元 | D. | 25元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a•3=b•3,则a=b类比推出 若a•0=b•0,则a=b | |
| B. | 若(a+b)c=ac+bc类比推出 $\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}$(c≠0) | |
| C. | 若(a+b)c=ac+bc类比推出 (a•b)c=ac•bc | |
| D. | 若(ab)n=anbn类比推出 (a+b)n=an+bn |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
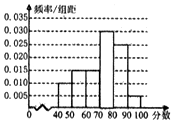 某中学选取20名优秀同学参加2015年英语应用知识竞赛,将他们的成绩(百分制)(均为整数)分成6组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.
某中学选取20名优秀同学参加2015年英语应用知识竞赛,将他们的成绩(百分制)(均为整数)分成6组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com