练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知函数y=$\frac{2kx+1}{k{x}^{2}+4x+3}$的定义域为R，求实数k的取值范围．

    分析 把函数y=$\frac{2kx+1}{k{x}^{2}+4x+3}$的定义域为R转化为对任意实数x，kx2+4x+3≠0恒成立，然后列出不等式组求解即可．

    解答 解：∵函数y=$\frac{2kx+1}{k{x}^{2}+4x+3}$的定义域为R，
    ∴kx2+4x+3≠0．
    ∴函数y=$\frac{2kx+1}{k{x}^{2}+4x+3}$与x轴无交点，
    即$\left\{\begin{array}{l}{k＞0}\\{△=16-12k＜0}\end{array}\right.$或$\left\{\begin{array}{l}k＜0\\△=16-12k＜0\end{array}\right.$，
    解得：$k＞\frac{4}{3}$．
    ∴k的取值范围是{k|k＞$\frac{4}{3}$}．

    点评 本题考查函数的定义域及其求法，考查了不等式的解法，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

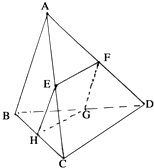    15．如图所示，四边形EFGH为四面体ABCD的一个截面，若四边形EFGH为平行四边形．
    （1）求证：AB∥平面EFGH；
    （2）若AB=4，CD=6，求四边形EFGH周长的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．设关于x的方程x2-2ax+a2-2a-3=0，试分别探究满足下列条件的实数a的取值范围．
    （1）方程有实根；
    （2）方程有两正根；
    （3）方程有一正一负根；
    （4）两根均大于0且小于1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知f（x）=$\left\{\begin{array}{l}{1-x-2{x}^{2}}&{x≤0}\\{|lgx|}&{x＞0}\end{array}\right.$若关于x的方程f（x）=a有四个实根x1，x2，x3，x4，则这四根之积x1，x2，x3，x4的取值范围是（　　）
    A．[0，$\frac{1}{2}$）B．[0，$\frac{1}{4}$）C．[0，$\frac{1}{8}$）D．[0，$\frac{1}{16}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．设f（x）=x2+px+q，A={x|f（x）=x}={p}，求p、q的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．α，β是两个不重合的平面，在下列条件中，可能判断平面α，β平行的是（　　）
    A．α，β都垂直于平面γB．平面γ与α，β均无公共点
    C．存在一条直线a，a?α，a∥βD．α内不共线的三点到β的距离相等

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．如图所示是一位同学画的一个实物的三视图，老师判断正视图是正确的，其他两个视图有错误，则正确的侧视图和俯视图是（　　）
    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．设f（x）=x•lnx，g（x）=ax-1，则：
    （1）若f（x）≥g（x）恒成立，求a的取值范围；
    （2）证明：y=$\frac{f（x）}{{x}^{2}}$没有过点P（0，1）的切线；
    （3）求证：ln（1+n）＞$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n+1}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知函数f（x）=x•sin（x+$\frac{π}{2}$），则f′（$\frac{π}{2}$）=-$\frac{π}{2}$．

    查看答案和解析>>

    同步练习册答案