
| A. | (1,2)或(-1,-2) | B. | (-1,-2) | C. | (2,1) | D. | (1,2) |
分析 设出$\overrightarrow{a}$的坐标表示,根据向量的模长公式与向量共线的坐标表示,列出方程组,即可求出$\overrightarrow{a}$的坐标.
解答 解:设$\overrightarrow{a}$=(x,y),
∵|$\overrightarrow{a}$|=$\sqrt{5}$,
∴x2+y2=5①,
又$\overrightarrow{b}$=(1,2),且$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴2x-y=0②,
由①、②组成方程组,解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,
所以$\overrightarrow{a}$的坐标为(1,2)或(-1,-2).
故选:A.
点评 本题考查了平面向量的坐标表示与应用问题,是基础题目.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:选择题
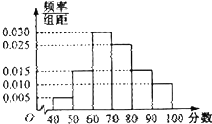 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )| A. | 588 | B. | 480 | C. | 450 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<-1或a>1 | B. | a≤-1或a≥1 | C. | a≥1 | D. | a>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y-1=0 | B. | x-2y+1=0 | C. | 2x+y-2=0 | D. | x+2y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
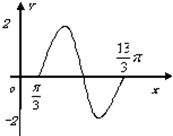 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<$\frac{π}{2}$)一段图象如图所示.
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<$\frac{π}{2}$)一段图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 结论正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com