Question

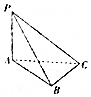
17．如图所示，三棱锥P-ABC中，PA⊥平面ABC，AB⊥BC，AB=1，BC=PA=2，则该几何体外接球的表面积为（　　）

• A． 4π
• B． 9π
• C． 12π
• D． 36π

Answer 1

分析 根据题意，证出BC⊥平面PAB，PC是三棱锥P-ABC的外接球直径．利用勾股定理结合题中数据算出PB得外接球半径，从而得到所求外接球的表面积．

解答 解：PA⊥平面ABC，AB⊥BC，∴BC⊥平面PAB，BC⊥PB
在Rt△PBA中，可得PB=$\sqrt{5}$，在Rt△PCA中，可得PC=$\sqrt{P{A}^{2}+A{C}^{2}}=\sqrt{{2}^{2}+{2}^{2}+{1}^{1}}=3$
取PB的中点O，则OA=OB=OC=OP=$\frac{3}{2}$
∴PC是三棱锥P-ABC的外接球直径；
几何体外接球的表面积4πR²=9π．
故选：B．

点评 本题在特殊三棱锥中求外接球的表面积，着重考查了线面垂直的判定与性质、勾股定理和球的表面积公式等知识，属于中档题．