
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
���� ������Բ�������ʵ�ȡֵ��Χ���ó���Բ�Ķ���Ķ��㹹�ɵĽǡ�F1BF2��ȡֵ��Χ���ֱ��жϣ�ʹ��PF1F2Ϊֱ�������εĵ�P������
��� 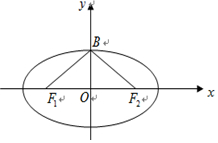 �⣺��ͼ��ʾ��حBF1ح=a��حOF1ح=c�����BF1O=�ȣ���tan��=$\frac{c}{a}$=e��
�⣺��ͼ��ʾ��حBF1ح=a��حOF1ح=c�����BF1O=�ȣ���tan��=$\frac{c}{a}$=e��
���У�����Բ��������0��e��$\frac{{\sqrt{2}}}{2}$ʱ����0��tan�ȣ�$\frac{{\sqrt{2}}}{2}$��
��ȡʣ�0��$\frac{��}{4}$�������F1BF2��$\frac{��}{2}$��
����PF1F2Ϊֱ��������ʱ��ֻ���ǡ�PF1F2�͡�PF2F1Ϊֱ��ʱ������
����������ֱ�������Σ�ֻ���ĸ���
���У�����Բ��������e=$\frac{{\sqrt{2}}}{2}$ʱ����tan��=$\frac{{\sqrt{2}}}{2}$��
���=$\frac{��}{4}$����ʱ��F1BF2=$\frac{��}{2}$����ʱ��Ӧ��ֱ�������ι���������
���У�����Բ��������$\frac{{\sqrt{2}}}{2}$��e��1ʱ����tan�ȣ�$\frac{{\sqrt{2}}}{2}$����ȡʣ�$\frac{��}{4}$��$\frac{��}{2}$����
��0����F1BF2��$\frac{��}{2}$����ʱ��Ӧ��ֱ�������ι��а˸���
��ѡD��
���� ����Ҫ��������Բ�ļ����������⣬���н�����漰��Բ�ı����̼���ļ������ʣ���Բ�������ʵ�֪ʶ����ۺϿ��飬���ؿ�����ѧ����������ͽ��������������Լ����ν��˼���Ӧ�ã������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2sin3 | B�� | -2sin3 | C�� | 2cos3 | D�� | -2cos3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
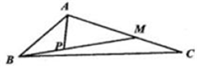 ��ͼ����֪��ABC�У���M���߶�AC�ϣ���P���߶�BM�ϣ�������$\frac{AM}{MC}$=$\frac{MP}{PB}$=2����|${\overrightarrow{AB}}$|=2��|${\overrightarrow{AC}}$|=3����BAC=120�㣬��$\overrightarrow{AP}$•$\overrightarrow{BC}$��ֵΪ-2��
��ͼ����֪��ABC�У���M���߶�AC�ϣ���P���߶�BM�ϣ�������$\frac{AM}{MC}$=$\frac{MP}{PB}$=2����|${\overrightarrow{AB}}$|=2��|${\overrightarrow{AC}}$|=3����BAC=120�㣬��$\overrightarrow{AP}$•$\overrightarrow{BC}$��ֵΪ-2���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com