
分析 利用通项公式可得有理项与无理项的项数.利用“插空法”及其排列公式即可得出概率.
解答 解:由二项式${(\sqrt{x}+\frac{1}{{2\root{4}{x}}})^8}$展开式的通项公式得:${T_{r+1}}=C_8^r{(\sqrt{x})^{8-r}}{(\frac{1}{{2\root{4}{x}}})^r}={(\frac{1}{2})^r}C_8^r{x^{\frac{16-3r}{4}}}$
可知当r=0,4,8时为有理项,其余6项为无理项.
展开式的9项全排列共有$A_9^9$种,
有理项互不相邻可把6个无理项全排列,把3个有理项在形成的7个空中插孔,有$A_6^6A_7^3$种.
故有理项都互不相邻的概率为$P=\frac{A_6^6A_7^3}{A_9^9}=\frac{5}{12}$.
故答案为:$\frac{5}{12}$.
点评 本题考查了二项式定理的应用、“插空法”、排列公式、概率计算公式,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
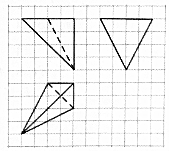 如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的体积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的体积为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{32}{3}$ | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | π | C. | 4π | D. | 16π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com