
分析 曲线C的极坐标方程化为直角坐标方程,得$\frac{{x}^{2}}{4}+{y}^{2}=1$,从而曲线C的参数方程为$\left\{\begin{array}{l}{x=2cosα}\\{y=sinα}\end{array}\right.$,0≤α<2π,设C上的点P(2cosα,sinα),求出P到直线x-2y-4$\sqrt{2}$=0的距离d=$\frac{2\sqrt{5}}{5}$|$\sqrt{2}$sin($α+\frac{3π}{4}$)-2$\sqrt{2}$|,由此能求出C上的点到直线x-2y-4$\sqrt{2}$=0的距离的最小值.
解答 解:∵曲线C的极坐标方程为ρ=$\frac{2}{\sqrt{1+3si{n}^{2}θ}}$,
∴ρ2+3ρ2sin2θ=4,
∴曲线C的直角坐标方程为x2+4y2=4,即$\frac{{x}^{2}}{4}+{y}^{2}=1$,
∴曲线C的参数方程为$\left\{\begin{array}{l}{x=2cosα}\\{y=sinα}\end{array}\right.$,0≤α<2π,
设C上的点P(2cosα,sinα),
P到直线x-2y-4$\sqrt{2}$=0的距离d=$\frac{|2cosα-2sinα-4\sqrt{2}|}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$|$\sqrt{2}$sin($α+\frac{3π}{4}$)-2$\sqrt{2}$|,
∴当sin($α+\frac{3π}{4}$)=1时,C上的点到直线x-2y-4$\sqrt{2}$=0的距离的最小值为dmin=$\frac{2\sqrt{10}}{5}$.
故答案为:$\frac{2\sqrt{10}}{5}$.
点评 本题考查极坐标方程、参数方程、普通方程的互化、求曲线上的点到直线距离的最小值等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查函数与方程思想、化归与转化思想,是中档题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
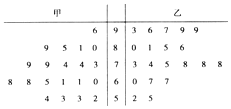 某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.| 甲班(A方式) | 乙班(B方式) | 总 计 | |
| 成绩优秀 | 1 | 5 | 6 |
| 成绩不优秀 | 19 | 15 | 34 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
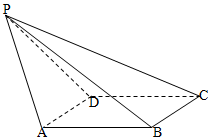 如图,已知四边形ABCD为菱形,平面ABCD外一点P,PB⊥AD,△PAD为边长等于2的正三角形,且PB在平面ABCD的射影长等于$\frac{3}{2}\sqrt{3}$.
如图,已知四边形ABCD为菱形,平面ABCD外一点P,PB⊥AD,△PAD为边长等于2的正三角形,且PB在平面ABCD的射影长等于$\frac{3}{2}\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},1]$ | B. | $(0,\frac{2}{3})$ | C. | $(\frac{2}{3},1]$ | D. | $(\frac{1}{2},\frac{2}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 |
| 人均纯收入y | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com