
分析 (1)可令x=$\frac{1}{2}$,计算即可得到所求;
(2)令x=$\frac{1}{n}$,求得f($\frac{1}{n}$)+f(1-$\frac{1}{n}$)=2011,再由倒序相加求和,即可得到an,再讨论a=1,a≠1,由错位相减法,即可得到所求;
(3)由$\frac{1}{{{{(n+1)}^2}}}<\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$,运用裂项相消求和,结合不等式的性质,即可得证.
解答 解:(1)由于函数f(x)对任意x∈R都有f(x)+f(1-x)=2011,
令$x=\frac{1}{2}$得:$f(\frac{1}{2})+f(1-\frac{1}{2})=f(\frac{1}{2})+f(\frac{1}{2})=2011$,
所以$f(\frac{1}{2})=\frac{2011}{2}$;
(2)令$x=\frac{1}{n}$,则$f(\frac{1}{n})+f(1-\frac{1}{n})=f(\frac{1}{n})+f(\frac{n-1}{n})=2011$.${a_n}=f(0)+f(\frac{1}{n})+f(\frac{2}{n})+…+f(\frac{n-2}{n})+f(\frac{n-1}{n})+f(1)$①
又${a_n}=f(1)+f(\frac{n-1}{n})+f(\frac{n-2}{n})+…+f(\frac{2}{n})+f(\frac{1}{n})+f(0)$②
两式相加得:$2{a_n}=[f(0)+f(1)]+[f(\frac{1}{n})+f(\frac{n-1}{n})]+[f(\frac{2}{n})+f(\frac{n-2}{n})]+…+[f(1)+f(0)]=2011(n+1)$,
即有${a_n}=\frac{2011(n+1)}{2}$.
∴$\frac{{2{a_n}{a^n}}}{2011}$=(n+1)an,
当a=1时,和Sn.=2+3+…+n+1=$\frac{1}{2}$n(n+3);
当a≠1时,和Sn=2a+3a2+..+(n+1)an,③
aSn=2a2+3a3+..+(n+1)an+1,④
③-④可得,(1-a)Sn=2a+a2+..+an-(n+1)an+1
=a+$\frac{a(1-{a}^{n})}{1-a}$-(n+1)an+1,
化简可得$\frac{a}{1-a}$+$\frac{a(1-{a}^{n})}{(1-a)^{2}}$-$\frac{(n+1)•{a}^{n+1}}{1-a}$.
则${S_n}=\left\{\begin{array}{l}\frac{n(n+3)}{2}(a=1)\\ \frac{a}{1-a}+\frac{{a(1-{a^n})}}{{{{(1-a)}^2}}}-\frac{{(n+1){a^{n+1}}}}{1-a}(a≠1)\end{array}\right.$;
(3)证明:∵$\frac{1}{{{{(n+1)}^2}}}<\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$,
∴$\frac{1}{{{a_n}^2}}=\frac{4}{{{{2011}^2}}}•\frac{1}{{{{(n+1)}^2}}}<\frac{4}{{{{2011}^2}}}(\frac{1}{n}-\frac{1}{n+1})$,
即有Tn=$\frac{1}{{{a}_{1}}^{2}}$+$\frac{1}{{{a}_{2}}^{2}}$+…+$\frac{1}{{{a}_{n}}^{2}}$<$\frac{4}{201{1}^{2}}$[(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$)]
=$\frac{4}{201{1}^{2}}$•(1-$\frac{1}{n+1}$)<$\frac{4}{201{1}^{2}}$.
点评 本题考查函数的性质和运用,考查数列的求和方法:倒序相加和错位相减法、裂项相消求和,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
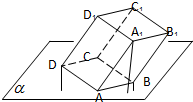 多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面α内,其余顶点在α的同侧,正方体上与顶点A相邻的三个顶点到α的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可能是:(2)(4)(5)(6).(写出所有正确结论的编号)
多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面α内,其余顶点在α的同侧,正方体上与顶点A相邻的三个顶点到α的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可能是:(2)(4)(5)(6).(写出所有正确结论的编号)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m?α,n?α,m∥n,则m∥α | B. | 若m⊥α,m?β,则α⊥β | ||
| C. | 若m?α,n?β,α∥β,则m∥n | D. | 若m⊥α,m⊥β,则α∥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com