Question

（2005•北京）设f（x）是定义在[0，1]上的函数，若存在x*∈（0，1），使得f（x）在[0，x•]上单调递增，在[x•，1]单调递减，则称f（x）为[0，1]上的单峰函数，x•为峰点，包含峰点的区间为含峰区间．

对任意的[0，1]上的单峰函数f（x），下面研究缩短其含峰区间长度的方法．

（Ⅰ）证明：对任意的x1，x2∈（0，1），x1＜x2，若f（x1）≥f（x2），则（0，x2）为含峰区间；若f（x1）≤f（x2），则（x1，1）为含峰区间；

（Ⅱ）对给定的r（0＜r＜0.5），证明：存在x1，x2∈（0，1），满足x2﹣x1≥2r，使得由（Ⅰ）确定的含峰区间的长度不大于0.5+r；

（Ⅲ）选取x1，x2∈（0，1），x1＜x2由（Ⅰ）可确定含峰区间为（0，x2）或（x1，1），在所得的含峰区间内选取x3，由x3与x1或x3与x2类似地可确定是一个新的含峰区间．在第一次确定的含峰区间为（0，x2）的情况下，试确定x1，x2，x3的值，满足两两之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34．

（区间长度等于区间的右端点与左端点之差）．

 

Answer 1

见解析

【解析】

试题分析：（Ⅰ）本题是一道新定义题，咋一看挺繁琐且无从下手，其实这类新定义题目只需牢牢的抓住题干定义，需要分f（x1）≥f（x2）和 f（x1）≤f（x2）两类情况讨论分析；

（Ⅱ）有了（Ⅰ）的讨论处理，第（Ⅱ）显的容易一些，只要借助（Ⅰ）用r把x1，x2分别表达出来；

（Ⅲ）本问题是在第（Ⅱ）问的基础上又提出的问题，关键是找出以下两组关系式：x1+x2=l和x3+x1=x2，

证明：（Ⅰ）设x*为f（x）的峰点，则由单峰函数定义可知，f（x）在[0，x*]上单调递增，在[x*，1]上单调递减．

当f（x1）≥f（x2）时，假设x*∉（0，x2），则x1＜x2＜x*，从而f（x*）≥f（x2）＞f（x1），

这与f（x1）≥f（x2）矛盾，所以x*∈（0，x2），即（0，x2）是含峰区间．

当f（x1）≤f（x2）时，假设x*∉（x1，1），则x*≤x1＜x2，从而f（x*）≥f（x1）＞f（x2），

这与f（x1）≤f（x2）矛盾，所以x*∈（x1，1），即（x1，1）是含峰区间．

（Ⅱ）由（Ⅰ）的结论可知：

当f（x1）≥f（x2）时，含峰区间的长度为l1=x2；

当f（x1）≤f（x2）时，含峰区间的长度为l2=1﹣x1；

对于上述两种情况，由题意得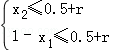①

由①得1+x2﹣x1≤1+2r，即x2﹣x1≤2r

又因为x2﹣x1≥2r，所以x2﹣x1=2r，②

将②代入①得

x1≤0.5﹣r，x2≥0.5﹣r，③

由①和③解得x1=0.5﹣r，x2=0.5+r．

所以这时含峰区间的长度l1=l1=0.5+r，即存在x1，x2使得所确定的含峰区间的长度不大于0.5+r．

（Ⅲ）【解析】
对先选择的x1；x2，x1＜x2，由（Ⅱ）可知

x1+x2=l，④

在第一次确定的含峰区间为（0，x2）的情况下，x3的取值应满足

x3+x1=x2，⑤

由④与⑤可得，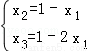

当x1＞x3时，含峰区间的长度为x1．

由条件x1﹣x3≥0.02，得x1﹣（1﹣2x1）≥0.02，从而x1≥0.34．

因此，为了将含峰区间的长度缩短到0.34，只要取x1=0.34，x2=0.66，x3=0.32．