
 平面
平面 ,四边形
,四边形 是矩形,
是矩形, ,
, ,点
,点 ,
, 分别是
分别是 ,
, 的中点.
的中点.
 的体积;
的体积;  平面
平面 ;
; 为线段
为线段 中点,求证:
中点,求证: ∥平面
∥平面 .
.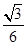 ;(Ⅱ)详见解析;(Ⅲ)详见解析
;(Ⅱ)详见解析;(Ⅲ)详见解析 平面
平面 ,所以
,所以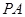 为三棱锥
为三棱锥 的高。因为
的高。因为 是矩形,所以可求底面
是矩形,所以可求底面 的面积,根据锥体体积公式
的面积,根据锥体体积公式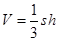 可求此三棱锥的体积。(Ⅱ)根据
可求此三棱锥的体积。(Ⅱ)根据 平面
平面 ,四边形
,四边形 是矩形,可证得
是矩形,可证得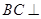 平面
平面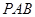 ,从而可得
,从而可得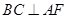 ,再根据等腰三角形中线即为高线可得
,再根据等腰三角形中线即为高线可得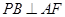 ,根据线面垂直的判定定理可得
,根据线面垂直的判定定理可得 平面
平面 。(Ⅲ)连结
。(Ⅲ)连结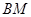 交
交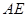 于
于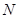 ,可证得
,可证得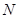 为
为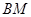 中点,由中位线可证得
中点,由中位线可证得 ∥
∥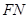 ,再由线面平行的判定定理可证得
,再由线面平行的判定定理可证得 ∥平面
∥平面 。
。 平面
平面 ,
,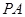 为三棱锥
为三棱锥 的高. 2分
的高. 2分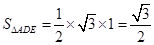 ,
,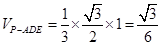 . 4分
. 4分 平面
平面 ,
,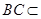 平面
平面 ,所以
,所以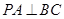 ,
, 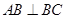 ,
,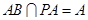 所以
所以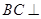 平面
平面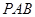
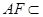 平面
平面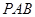 , 所以
, 所以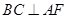 . 6分
. 6分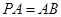 ,点
,点 是
是 的中点,所以
的中点,所以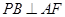 ,又因为
,又因为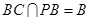 ,
, 平面
平面 . 8分
. 8分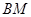 交
交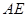 于
于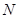 ,连结
,连结 ,
,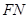 .
.
 是矩形,所以
是矩形,所以 ,且
,且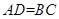 ,
, ,
, 分别为
分别为 ,
, 的中点, 所以四边形
的中点, 所以四边形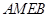 是平行四边形,
是平行四边形,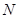 为
为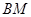 的中点,又因为
的中点,又因为 是
是 的中点,
的中点, ∥
∥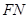 , 13分
, 13分 平面
平面 ,
,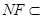 平面
平面 ,
, ∥平面
∥平面 . 14分
. 14分

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
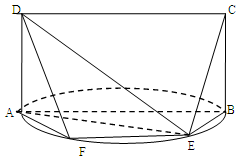
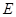 是以
是以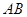 为直径的半圆上异于点
为直径的半圆上异于点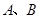 的点,矩形
的点,矩形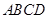 所在的平面垂直于该半圆所在平面,且
所在的平面垂直于该半圆所在平面,且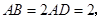
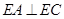 ;
;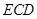 与半圆弧的另一个交点为
与半圆弧的另一个交点为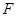 ,
,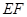 //
//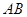 ;
;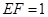 ,求三棱锥E-ADF的体积.
,求三棱锥E-ADF的体积.查看答案和解析>>
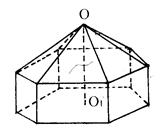
科目:高中数学 来源:不详 题型:填空题
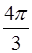 ,则圆锥的体积是________
,则圆锥的体积是________ .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com