
【题目】已知函数![]() ,
,![]() ,
,
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的单调性并判断有无极值,有极值时求出极值.
的单调性并判断有无极值,有极值时求出极值.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)欲求曲线![]() 在点
在点![]() 处的切线方程,只需求出斜率
处的切线方程,只需求出斜率![]() 和和
和和![]() 的值,即可利用直线的点斜式方程求解切线的方程;
的值,即可利用直线的点斜式方程求解切线的方程;
(2)求出![]() ,通过讨论
,通过讨论![]() 的取值范围,求出函数的单调区间,从而求出函数的极值即可,可分
的取值范围,求出函数的单调区间,从而求出函数的极值即可,可分![]() 两种情况,求出函数的单调区间,得出函数的极值.
两种情况,求出函数的单调区间,得出函数的极值.
试题解析:
(1)![]() 时,
时,![]() ,
,![]()
所以![]() ,
,![]()
因此曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]()
即![]()
(2)![]()
![]()
①当![]() 时,
时,![]() 恒成立,
恒成立,
所以当![]() 时
时![]() ,
,![]() 单调递减
单调递减
当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
所以当![]() 时,
时,![]() 取极小值
取极小值![]()
②当![]() 时,由
时,由![]() 得
得![]() 或
或![]()
(ⅰ)当![]() ,即
,即![]() 时
时
由![]() 得
得![]() 或
或![]()
由![]() 得
得![]()
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,故
上单调递增,故![]() 时,
时,![]() 取极大值
取极大值![]() ,
,![]() 时,
时,![]() 取极小值
取极小值![]()
(ⅱ)当![]() ,即
,即![]() 时,
时,![]() 恒成立
恒成立
此时函数![]() 在
在![]() 上单调递增,函数
上单调递增,函数![]() 无极值
无极值
(ⅲ)当![]() ,即
,即![]() 时
时
由![]() 得
得![]() 或
或![]()
由![]() 得
得![]()
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,故
上单调递增,故![]() 时,
时,![]() 取极大值
取极大值![]()
![]() 时,
时,![]() 取极小值
取极小值![]() .
.


科目:高中数学 来源: 题型:
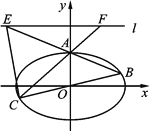
【题目】如图,在平面直角坐标系![]() 中,椭圆:
中,椭圆: ![]() 的离心率为
的离心率为![]() ,直线l:y=2上的点和椭圆上的点的距离的最小值为1.
,直线l:y=2上的点和椭圆上的点的距离的最小值为1.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 已知椭圆的上顶点为A,点B,C是上的不同于A的两点,且点B,C关于原点对称,直线AB,AC分别交直线l于点E,F.记直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() .
.
① 求证: ![]() 为定值;
为定值;
② 求△CEF的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数y=f(x),当x≥0时,f(x)=x2﹣2x. 
(1)求当x<0时,函数y=f(x)的解析式,并在给定坐标系下,画出函数y=f(x)的图象;
(2)写出函数y=|f(x)|的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发一种新药,如果成年人按规定的剂量服用,据监测,服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.据进一步测定,每毫升血液中含药量不少于0.25微克时,治疗疾病有效,则服药一次治疗该疾病有效的时间为( ) 
A.4小时
B.![]()
C.![]()
D.5小时
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为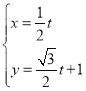 (
(![]() 为参数),曲线
为参数),曲线![]() 的普通方程为
的普通方程为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(I)求直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的参数方程;
的参数方程;
(II)设点D在曲线![]() 上,且曲线
上,且曲线![]() 在点D处的切线与直线
在点D处的切线与直线![]() 垂直,试确定点D的坐标.
垂直,试确定点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com