
 ��ͼ���ں�����EFһ����һ�������ֳ������ֳ���ǰһ���ֱ߽�Ϊ���߶�FGBC�������߶��Ǻ���y=Asin����x+�գ���A��0���أ�0���աʣ�0���У�����x��[-4��0]��ͼ��ͼ�����ߵ�ΪB��-1��2�����߽���м䲿��Ϊ��1ǧ��ֱ�߶�CD����CD��EF�����ֳ��ĺ�һ���ֱ߽�����OΪԲ�ĵ�һ��Բ��$\widehat{DE}$��
��ͼ���ں�����EFһ����һ�������ֳ������ֳ���ǰһ���ֱ߽�Ϊ���߶�FGBC�������߶��Ǻ���y=Asin����x+�գ���A��0���أ�0���աʣ�0���У�����x��[-4��0]��ͼ��ͼ�����ߵ�ΪB��-1��2�����߽���м䲿��Ϊ��1ǧ��ֱ�߶�CD����CD��EF�����ֳ��ĺ�һ���ֱ߽�����OΪԲ�ĵ�һ��Բ��$\widehat{DE}$������ ��1��������ɵ�A=2��T=12���������ϕ���Ӷ������ʽ��
��2������$y=2sin��\frac{��}{6}x+\frac{2��}{3}��$=1���x���Ӷ���·GO�ij���
��3����ͼ��Sƽ���ı���OMPQ=OM•PP1=$��2cos��-\frac{2\sqrt{3}}{3}sin�ȣ�•2sin��$=$4sin��cos��-\frac{4\sqrt{3}}{3}si{n}^{2}��$=$2sin2��+\frac{2\sqrt{3}}{3}cos2��-\frac{2\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}sin��2��+\frac{��}{6}��-\frac{2\sqrt{3}}{3}$���Ӷ�����ֵ��
��� �⣺��1������֪��������A=2��
�֡�$\frac{T}{4}=3$��$T=\frac{2��}{��}=12$����$��=\frac{��}{6}$��
�֡ߵ�x=-1ʱ����y=2sin��-$\frac{��}{6}$+�գ�=2�����=$\frac{2��}{3}$��
�����߶�FGBC�Ľ���ʽΪ$y=2sin��\frac{��}{6}x+\frac{2��}{3}��$��x��[-4��0]��
��2����$y=2sin��\frac{��}{6}x+\frac{2��}{3}��$=1
��x=6k+��-1��k-4 ��k��Z����
��x��[-4��0]����k=0��x=-3����G��-3��1����
��OG=$\sqrt{10}$��
�ྰ��·GO��Ϊ$\sqrt{10}$ǧ�ף�
��3����ͼ��OC=$\sqrt{3}$��CD=1����OD=2��$��COD=\frac{��}{6}$��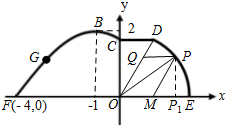
��PP1��x����P1�㣬��Rt��OPP1�У�PP1=OPsin��=2sin�ȣ�
�ڡ�OMP�У�$\frac{OP}{sin120��}=\frac{OM}{sin��60��-�ȣ�}$��
��$OM=\frac{OP•sin��60��-�ȣ�}{sin120��}=\frac{4}{\sqrt{3}}•sin��60��-�ȣ�$=$2cos��-\frac{2\sqrt{3}}{3}sin��$��
Sƽ���ı���OMPQ=OM•PP1=$��2cos��-\frac{2\sqrt{3}}{3}sin�ȣ�•2sin��$
=$4sin��cos��-\frac{4\sqrt{3}}{3}si{n}^{2}��$=$2sin2��+\frac{2\sqrt{3}}{3}cos2��-\frac{2\sqrt{3}}{3}$
=$\frac{4\sqrt{3}}{3}sin��2��+\frac{��}{6}��-\frac{2\sqrt{3}}{3}$ �ȡʣ�0��$\frac{��}{3}$����
��$2��+\frac{��}{6}=\frac{��}{2}$ʱ����$��=\frac{��}{6}$ʱ��ƽ���ı���������ֵΪ$\frac{2\sqrt{3}}{3}$��
���� ���⿼�������Ǻ�����ʵ�������е�Ӧ�ã�������ѧ������ͼ�����������е��⣮


 ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | k��$\frac{3}{4}$��k��-4 | B�� | k��$\frac{3}{4}��k��-\frac{1}{4}$ | C�� | -4��k��$\frac{3}{4}$ | D�� | $\frac{3}{4}$��k��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 6 | C�� | 7 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������P-ABCD�У�����ABCD�Ǿ��Σ�PA��ƽ��ABCD��AP=AB��BP=BC=2��E��F�ֱ���PB��PC���е㣮
��ͼ��������P-ABCD�У�����ABCD�Ǿ��Σ�PA��ƽ��ABCD��AP=AB��BP=BC=2��E��F�ֱ���PB��PC���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com