考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的概念及应用
分析:(1)对于第一问非常简单,只需按求解极值的定义求解即可.
(2)在所给式子中含绝对值,一般考虑去掉绝对值,x1,x2是任给的两个数,所以可考虑用函数单调性.去掉绝对值之后,注意观察式子,你会发现,只要做适当变形,便可利用函数单调性的定义,得到一个新的函数的单调性,再结合导数求a的范围即可.
(3)通过第三问的条件,你会得到f(x)在区间(0,e]不是单调函数的结论,并要求f(x)的值域需包含g(x)的值域便可.接下来就是看怎样让f(x)的值域包含g(x)的值域,即能求出m的范围.
解答:
解:(1)g′(x)=
,令
=0,解得x=1,
∵e
x>0,∴x∈(-∞,1)时,g′(x)>0;x∈(1,+∞)时,g′(x)<0,根据极大值的定义知:g(x)极大值是g(1)=1,无极小值.
(2)当m=1,a<0时,f(x)=x-alnx-1,所以在[3,4]上f′(x)=
>0,所以f(x)在[3,4]上是增函数.
设h(x)=
=,所以在[3,4]上h′(x)=
>0,所以h(x)在[3,4]上为增函数.
设x
2>x
1,则
|f(x2)-f(x1)|<|-|恒成立,变成
f(x2)-f(x1)<-恒成立,即:f(x
2)-f(x
1)<h(x
2)-h(x
1)恒成立,即:f(x
2)-h(x
2)<f(x
1)-h(x
1).设u(x)=f(x)-h(x)=
x-alnx-1-•,则u(x)在[3,4]上为减函数.
∴u′(x)=1-
-•≤0在[3,4]上恒成立.
∴
a≥x-ex-1+恒成立.设v(x)=x-
-ex-1+,所以v′(x)=1-
ex-1+=
1-ex-1[(-)2+],因为x∈[3,4],所以
ex-1[(-)2+]>e2,所以v′(x)<0,所以v(x)为减函数.
∴v(x)在[3,4]上的最大值为v(3)=
3-e2.
∴a≥
3-e2,∴a的最小值为:
3-e2.
(3)由(1)知g(x)在(0,1]上单调递增,在(1,e]单调单调递减,又g(0)=0,g(e)=
,所以g(x)的值域是(0,1].
∵f(x)=mx-2lnx-m;
∴当m=0时,f(x)=-2lnx,在(0,e]为减函数,由题意知,f(x)在(0,e]不是单调函数;故m=0不合题意;
当m≠0时,f′(x)=
,由于f(x)在(0,e]上不单调,所以
0<<e,即
m>;①
此时f(x)在(0,
)递减,在(
,e]递增;
∴f(e)≥1,即me-2-m≥1,解得
m≥;②
所以由①②,得
m≥;
∵1∈(0,e],∴f(
)≤f(1)=0满足条件.
下证存在t∈(0,
]使得f(t)≥1;
取t=e
-m,先证
e-m<,即证2e
m-m>0;③
设w(x)=2e
x-x,则w′(x)=2e
x-1>0在[
,+∞)时恒成立;
∴w(x)在[
,+∞)上递增,∴w(x)≥
w()>0,所以③成立;
再证f(e
-m)≥1;
∵f
(e-m)=me-m+m>m≥>1,∴
m≥时,命题成立.
所以m的取值范围是:[
,+∞).
点评:本题用到的知识点有:1.极值的定义.
2.用倒数求函数单调区间,判断单调性的方法.
3.单调函数定义的运用.
4.会对式子做适当变形,从而解决问题.



 阅读快车系列答案
阅读快车系列答案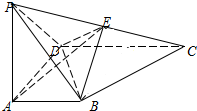 如图,在四棱锥P-ABCD中,AD=CD=2AB=2,PA⊥AD,AB∥CD,CD⊥AD,E为PC的中点,且DE=EC.
如图,在四棱锥P-ABCD中,AD=CD=2AB=2,PA⊥AD,AB∥CD,CD⊥AD,E为PC的中点,且DE=EC.