
分析 (1)化简a7a8=27a${\;}_{9}^{2}$可得a7=27a10,从而求得$q=\frac{1}{3}$,从而写出{an}的通项公式;
(2)利用对数运算化简可得log3a2n+1=-2n,log3a2n+3=-2n-2,从而利用裂项求和法求和.
解答 解:(1)∵a7a8=27a${\;}_{9}^{2}$,∴a7a8=27a8a10,
∴a7=27a10,
设{an}的公比为q,则${q^3}=\frac{{{a_{10}}}}{a_7}=\frac{1}{27}$,
故$q=\frac{1}{3}$,
所以{an}的通项公式为an=($\frac{1}{3}$)n-1;
(2)log3a2n+1=log3(($\frac{1}{3}$)2n)=-2n,
log3a2n+3=log3(($\frac{1}{3}$)2n+2)=-2n-2,
故bn=-$\frac{1}{lo{g}_{3}{a}_{2n+1}•lo{g}_{3}{a}_{2n+3}}$=-$\frac{1}{4n(n+1)}$=-$\frac{1}{4}$($\frac{1}{n}$-$\frac{1}{n+1}$),
故${S_n}=-\frac{1}{4}[{(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+…+(\frac{1}{n}-\frac{1}{n+1})}]=-\frac{1}{4}(1-\frac{1}{n+1})=-\frac{n}{4n+4}$.
点评 本题考查了数列的性质的判断与应用,同时考查了对数运算及裂项求和法的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$+1 | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,$\frac{2}{3}$] | B. | [-$\frac{1}{3}$,2) | C. | (-∞,$\frac{2}{3}$] | D. | [-$\frac{2}{3}$,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
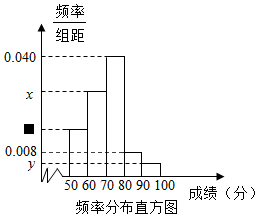 某中学为了解某次竞赛成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题:
某中学为了解某次竞赛成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题:| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 9 | 0.18 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | ▓ | 0.08 |
| 第5组 | [90,100] | 2 | b |
| 合计 | ▓ | ▓ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<4} | B. | {x|-2<x<3} | C. | {x|-2<x<-1} | D. | {x|-2<x<-1或3<x<4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com